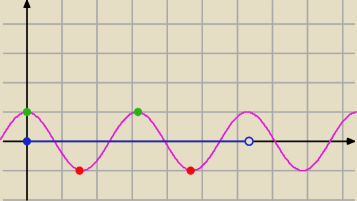
 Dziś może takie rozwiązanie: warunek to równanie okręgu; możemy więc przyjąć x=cosα, y=sinα.
Wówczas f(x,y)=f(cosα,sinα) = cos2α, dla α∊[0,2π) (przedział niebieski na rysunku).
Funkcja ta ma więc
a) dwa maksima lokalne (na rysunku na zielono) odpowiadające przypadkowi, gdy α=0 lub α=π
(wówczas (x,y)=(1,0) lub (x,y)=(−1,0))
b) dwa minima lokalne (na rysunku na czerwono) odpowiadające przypadkowi, gdy α=π/2 lub α=3π/2
(wówczas (x,y)=(0,1) lub (x,y)=(0,−1))
Dziś może takie rozwiązanie: warunek to równanie okręgu; możemy więc przyjąć x=cosα, y=sinα.
Wówczas f(x,y)=f(cosα,sinα) = cos2α, dla α∊[0,2π) (przedział niebieski na rysunku).
Funkcja ta ma więc
a) dwa maksima lokalne (na rysunku na zielono) odpowiadające przypadkowi, gdy α=0 lub α=π
(wówczas (x,y)=(1,0) lub (x,y)=(−1,0))
b) dwa minima lokalne (na rysunku na czerwono) odpowiadające przypadkowi, gdy α=π/2 lub α=3π/2
(wówczas (x,y)=(0,1) lub (x,y)=(0,−1))