z parametrem SiA: Zastanawiam się nad tym zadaniem:

	2x−b−5
Dla jakich wartości parametru m nierówność		< O jest spełniona przez
	3x+b+5

wszystkie liczby rzeczywiste x takie, że |x| ≤ 2? ma ktoś jakiś pomysł ?

SiA: wie ktoś ?

3Silnia&6: rownanie nie ma parametru m, wiec wiadomo dla parametru b, rozumiem tak b+5 = k (2x − k)(3x + k) < 0 dla lxl ≤ 2, czy to jest mozliwe ? Tak jesli jedym pierwiastekiem bedzie 2 , drugim −2. k/2 = 2 i k/3 = 2 ? oj nie. Nie ma rozwiazania.

SiA: ja to zaczęłam tak robić (2x−b−5)(3x+b+5)<0 po przemnożeniu wyszło mi 6x²−(b+5)−b²−10b−25<0 (*) i postawiłam warunki : nierówność (*) jest spełniona przez wszystkie liczby rzeczywiste x, takie że IxI≤2 ⇔Δ>0 i x1 >−2 i x2 <2 dobrze?

pigor: ..., wychodzi mi b∊{−1,1,−9,−11}, a co ... masz w odpowiedziach

Kacper: Fajne zadanko

SiA: niestety do tego zadania nie mam odpowiedzi a pigor jak to wyliczyłeś ?

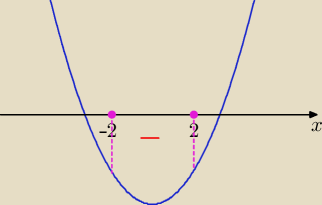
Eta: (2x−b−5)(3x+b+5) <0 i |x|≤2⇔x∊<−2,2> Parabola ramionami do góry To warunkiem spełniającym treść zadania jest: f(−2)<0 i f(2)<0 Rozwiąż układ nierówności (−4−b−5)(−6+b+5)<0 ⇒ (b+9)(b−1) >0 ⇒ b∊ ...... i (4−b−5)(6+b+5)<0 ⇒ (b+1)(b+11) >0 ⇒ b∊ .... część wspólna obydwu rozwiązań będzie odpowiedzią ..........