. ania: określ dziedzinę funkcji f(x) √2−x−x² / x więc x≠0 i 2−x−x² ≥0 x²−x−2≤0 i tu jak wylicze delte i x1 i x2 to mam zapisać,że x∊R− {0, x1, x2} ?

J: nie, musisz wyznaczyć przedziały

ania: to ja już nie wiem :C

J: dla jakich x , x² − x − 2 ≥ 0 ?

Grzeniuu: x² − x − 2 ≤ 0 Δ=9 x₁ =1 x₂ =−2 rysujemy wykres i otrzymujemy ze x∊ <−2 ; 1> ale nie moze byc 0 wiec uwzględniamy to i otrzymujemy ze x∊<−2;0)u(0;1>

ania: ale to obliczać z delty?

ania: NO WŁAŚNIE, dziękuje!

J: nie pisz Grzeniuu bzdur

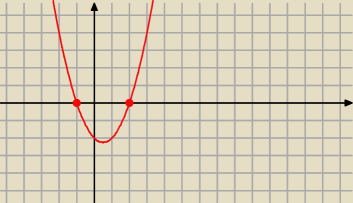
5-latek: Δ=9 to x₁= 2 i x₂= −1 To jest wykres funkcji y=x²−x−2 teraz patrz gdzie jest ona≤0(w jakim przedziale

Grzeniuu: z delty trzeba wyciągnąć jeszcze pierwiastek czyli bedzie 3

J: ma być ≥ 0

ania: ale mnoży się przez minus tam na początku, zmienia się znak

J: popatrz na wykres 5−ciolatka

5-latek: J ale zmienila znak na + przy x² i zmienil sie zwrot nierownosci

Grzeniuu: przepraszam moj blad pieriwatkami beda 2 i −1 , machnołem sie w obliczeniach

J: małolat .. .wyjaśnij im to , bo błądzą..

J: cholera ... nie zaważyłem

Grzeniuu: x∊<−1;0)u(0;2>

ania: ale to wszystko mnoży się przez minus, powinno być x²+x−2<0 wtedy bedzie, ze x∊<−2,0)u(0,1>

5-latek: Grzesiek czy w tych przedzialach x lezy pod osia OX bo ma byc ≤0?

ania: może ktoś mi napisać to dokładnie, bo już mam kilka różnych wersji i nie wiem, która jest na pewno prawidłowa

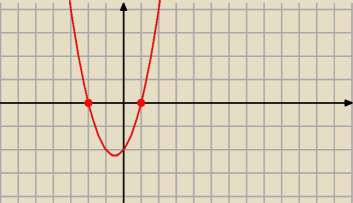
5-latek: Tak Aniu masz racje bo ja tez przepisalem tak jak napisano czyli mamy x²+x−2

	−1+3		−1−3
delta = 9 √9=3 i x1=		= 1 i x2=		= −2
	2		2

Teraz w jakim przedziale x_sy leza pod osia OX?

5-latek: Aniu ale nierownosc kwadratowa powinnas sama umiec rozwiazac bez zadnych wersji

ania: już wszystko rozumiem,dziękuje

5-latek: To napisz jaki to przedzial