punkt przecięcia prostych należący do okręgu K: Dla jakich wartości parametru m proste k: 2x−5y−m−6=0 i p: x−y−m+3=0 przecinają sie w punkcie, który należy do okręgu S(2,1) i promieniu r=√5. Próbowałam zrobić z tych prostych układ równań, żeby x i y uzależnić od m, potem podstawić do wzoru okręgu (x−2)² +(y−1)²=5 Jak powinnam zrobić tego typu zadanie i dlaczego mój pomysł nie zadziałał?

Eve: dobry pomysł, trzeba rozwiązać układ 3 równań: proste i okrąg, masz 3 niewiadome, musi sie udać

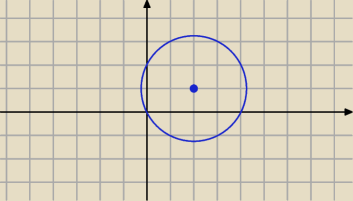
Mila: k: 2x−5y−m−6=0 i p: x−y−m+3=0 2x−5y=m+6 x−y=m−3 /*(−2) 2x−5y=m+6 −2x+2y=−2m+6 +========== −3y=−m+12

	1
y=		m−4
	3

	1
x−(		m−4)=m−3
	3

	4		1
x=		m−7 i y=		m−4 i x,y∊okręgu: (x−2)2 +(y−1)2=5
	3		3

	4		1
(		m−7−2)2+(		m−4−1)2=5⇔
	3		3

	4		1
(		m−9)2+(		m−5)2=5
	3		3

Δ<0 Sprawdź czy dobrze zapisałaś treść, znaki i sformułowania, może punkt przecięcia ma leżeć w kole ?

Eta: