pomożcie. mieszko: Obwód trapezu równoramiennego opisanego na okręgu jest równy 16, a przekątna trapezu ma długość 5. Oblicz długość promienia okręgu wpisanego w ten trapez i promienia okręgu opisanego na nim.

Bogdan: Dobry wieczór. a = |AB|, b = |CD|, c = |BC| = |AD| = x + y 4x + 4y = 16 ⇒ x + y = 4 ⇒ c = 4 Trapez jest opisany na okręgu o promieniu r > 0 ⇒ r² = xy oraz a + b = 2c ⇒ a + b = 8

	a + b		8
|AE| =		=		= 4
	2		2

Z tw. Pitagorasa w ΔAEC: h = √5² − 4² = 3 Z tw. Pitagorasa w ΔEBC: |EB| = √4² − 3² = √7 a = |AE| + |EB| = 4 + √7 oraz b = 8 − a = 4 − √7

	b		4 − √7		a		4 + √7
x =		=		oraz y =		=
	2		2		2		2

	4 − √7		4 + √7		9		3
r2 =		*		=		⇒ r =
	2		2		4		2

Okrąg o promieniu R jest opisany na trapezie ABCD i jednocześnie na trójkącie ABC.

	1		3
Pole ΔABC PΔ =		(4 + √7)*3 =		(4 + √7)
	2		2

	a*c*5		(4 + √7)*4*5		10
R =		=		=
	4PΔ		3   4* (4 + √7)   2		3

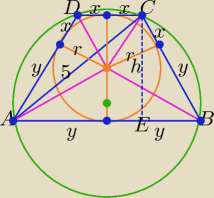
Eta: Po 6−ciu latach podam takie rozwiązanie tego zadania( wykorzystując rys. Bogdana |AB|=a , |DC|=b , |AD|=|BC|=c , |AC|=5 , h=2r , L=16 Z warunku wpisania okręgu w trapez:

	a+b
a+b=2c z treści zadania 2(a+b)=16 ⇒		=4 to c=4
	2

	a+b
|AE|=		= 4
	2

	3
z tw. Pitagorasa w ΔAEC ; h= √25−16= 3 ⇒ r=
	2

Okrąg o promieniu R opisany na trapezie jest jednocześnie opisany na Δ ABC |∡EAC|=|∡BC|=α

	h		3
W ΔAEC : sinα=		=
	5		5

z tw. sinusów w ΔABC :

	c		5		10
2R=		⇒ 2R=4*		⇒ R=
	sinα		3		3