kąty trójkąta ig: Okrąg podzielono na trzy części w stosunku 5:6:7 i przez punkty podziału poprowadzono styczne. Wyznacz miary kątów otrzymanego trójkąta.

Eta: Pomagam .... rysuję ... cierpliwości...

mieszko: okk czekam

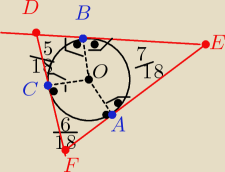
Eta: Przepraszam ,ale miałam ważny telefon Zatem: Podział okręgu na łuki : jest w stosunku : łuk AB : ⁷₁₈ łuk BC ; ⁵₁₈ łuk CA: ⁶₁₈ więc: kąty: środkowe odpowiadające tym łukom mają miary: kąt BOA = ⁷₁₈*360^o = 140^o kąt COB= ⁵₁₈*360^o = 100^o kąt COA= ⁶₁₈*360^o = 120^o czworokąty BOAE i COAF i COBD mają po dwa kąty przeciwległe o miarach po 90^o więc kąt E = 180^o − kąat BOA = 180^o− 140^o = 40^o kąt F = 180^o − kąt COA= 180^o −120^o = 60^o kąt D = 180^o − kąt COB = 180^o − 100^o = 80^o

Eta: Rysunek , troszkę nieczytelny: Zaznacz wszystkie kąty proste między promieniami a stycznymi w tych czworokątach

mieszko: dziękuje

michał : nie za dobrze rozumiem dlaczego tam jest każda wartość [stosunku] dzielona przez 18, skąd to 18 się wzięło?

Mila: x− wspólna miara 5x+6x+7x=18x

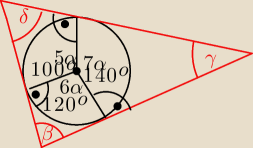
Gustlik: Najprościej tak: 5α+6α+7α=360^o 18α=360^o /:18 α=20^o stąd katy środkowe: 5α=100^o, 6α=120^o, 7α=140^o Nietrudno zauważyć, że promienie podzieliły ten trójkąt na 3 deltoidy, każdy z tych deltoidów ma po 2 kąty = 90^o, zatem w każdym z nich suma kąta środkowego i kąta przeciwległego do niego =180^o, Zatem β+120^o=180⁰⇔β=60^o γ+140^o=180⁰⇔γ=40^o δ+100^o=180^o⇔δ=80^o