Podaj zbiór rozwiązań nierówności.
Apocalipto: Podaj zbiór rozwiązań nierówności f(x) ≤ g(x)
Jakie wzory lub przekształcenia użyć zwłaszcza w g(x)?
6 lut 20:08
Apocalipto: Jakieś wskazówki?
6 lut 20:14
Marcin:
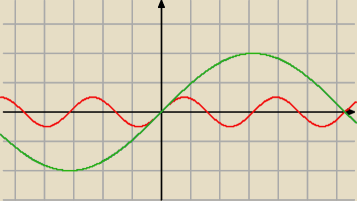
6 lut 20:32
Apocalipto: Nie da się tego zrobić obliczeniowo?
6 lut 20:54
Godzio:
| 1 | | 1 | | 1 | | 1 | |
| sin2x = sinxcosx = 2sin |
| xcos |
| xcosx ≤ 2sin |
| x |
| 2 | | 2 | | 2 | | 2 | |
| | 1 | | 1 | |
⇔ sinx |
| x(cos |
| xcosx − 1) ≤ 0 |
| | 2 | | 2 | |
Oczywiście wyrażenie w nawiasie będzie zawsze
niedodatnie. Dlaczego?
| | 1 | |
Wystarczy zatem sprawdzić kiedy sin |
| x ≥ 0 |
| | 2 | |
x = 2kπ
Stąd x ∊ <2kπ,2π + 2kπ>
6 lut 21:05
Godzio:
Mała pomyłka: x ∊ <4kπ, 2π + 4kπ>
6 lut 21:06
Apocalipto: Dziękuje bardzo za pomoc.

6 lut 21:29

