parzystosc /nieparzystosc
5-latek:
Zadanie :
a)Uzasadnij ze nie ma wektora niezerowego takiego ,ze przesuwajac o niego wykres dowolnej
funkcji nieparzystej otrzymamy wykres funkcji nieparzystej
Nie rozumiem tego polecenia gdyz zaraz mam nastepne
b) Podaj przyklad funkcji nieparzystej i takiego przesuniecia ze funkcja przesuniecia tez jest
nieparzysta
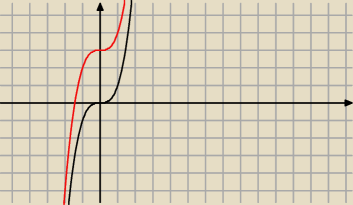
Co do b) to jesli wezniemy np y=x
3 i przesuniemy ja o wektor np [0 3] to dostanniemy funkcje
nieparzysta
6 lut 19:20
5-latek: Co do a) dlatego napisalem ze nie rozumiem tego polecenia gdyz w b) pokazalem ze jest taki
wektor
6 lut 19:30
Saizou :
co do a)
załóżmy że istnieje taki wektor [a,b], wówczas translacja o wektor funkcji f(x) będzie wyglądać
następująco g(x)=f(x−a)+b, zatem
−[f(x−a)+b]=−f(x−a)−b oraz f(−(x−a))+b=f(a−x)+b stąd −g(x)≠g(−x)
6 lut 19:40
Gray: Twoje rozwiązanie b) jest złe. Ta funkcja po przesunięciu nie jest nieparzysta.
Co do a). Nie jest to prawdą: funkcja f(x)≡0 jest nieparzysta; przesuwając ją o dowolny wektor
postaci (p,0), otrzymujesz funkcję f(x−p) ≡0 więc jest to również funkcją nieparzystą.
Mniej trywialny przykład? Bardzo proszę: f(x)=sinx, wektor u=(2π,0).
To jest również uzasadnienie b)
6 lut 19:42
Saizou :
zapomniałem o założeniu że a,b≠0
6 lut 19:42
5-latek: Czesc
Saizou 
dzieki za rozpisanie (nie jestem mocny w tym
A jak sesja (pozaliczane wszystko ?
6 lut 19:43
Gray: Nie "a,b≠0" tylko "a≠0 lub b≠0".
6 lut 19:45
Saizou :
To miałem na myśli
Gray 
5−latek sesja jak sesja, został mi jeszcze jeden egzamin 16, ale na razie wszystko
zaliczone
6 lut 19:46
5-latek: Gray
Co do b) to mnie troche podlamales bo myslalem ze jest
czyli aby funkcja byle nieparzysta to musi byc swoim odbiciem wzgledem poczatku ukladu
wspolrzednych
6 lut 19:53
Gray: Tak musi być, ale ta Twoja nie jest po przesunięciu symetryczna.
6 lut 21:28
5-latek: Dobrze
6 lut 21:33
5-latek: Jutro jeszcze powtarzam sobie caly ten material o funkcjach i biore sie za liniowe
6 lut 21:37
6 lut 21:37
5-latek: Poczytam sobie to jeszcze
Milu
Tam na tym medianauka w tamtym roku mialem chyba wykupione konto
A co do naszego forum to Jakub powinien dolaczyc kilka zadan
6 lut 21:42