proszę o rozwiązanie
Michał: Jedna z przyprostokątnych trójkąta prostokątnego ma długość a a odcinek dwusiecznej kąta
| | a2d | |
prostego zawarty w trójkącie ma długość d√2 Udowodnij że PΔ = |
|
|
| | 2(a −d) | |
ja to rozpocząłem tak
ΔABC − prostokątny D∊ ICBI I AD I = d
√2 IACI = a , IBCI = b ,
IEDI II IABI i IDFI II IACI
∠DAB == 45
0
| | 1 | |
PΔABC = |
| * a*b = PΔADC + PΔABC
|
| | 2 | |
| 1 | | 1 | | 1 | |
| * a*b = |
| *a* IDEI + |
| *b* IDFI
|
| 2 | | 2 | | 2 | |
AFDE jest kwadratem ponieważ IAD I = d
√2 nie mogę obliczyć IA EI bo ten odcinek po
obliczeniu jest równy IADI a to jest sprzeczne może moje rozumowanie jest niewłaściwe
6 lut 19:15
Mila:
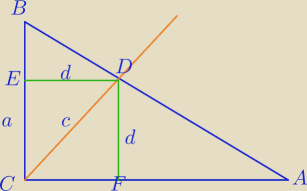
|BC|=a
|DC|=d
√2
|BE|=a−d
d<a
ΔBED∼ΔBCE⇔
| | 1 | | 1 | | ad | |
PΔABC= |
| a*b= |
| *a* |
| ⇔ |
| | 2 | | 2 | | a−d | |
cnw
===============
6 lut 19:56
Michał: jak poznać z tekstu że oznaczenia na rysunku są błędne
u mnie zamiast C jest A zamiast A jest B
bo z Twojego rysunku to jest zgodne
6 lut 20:11
Michał: w piątej linijce powinno chyba być ΔBED ≈ Δ ABC
6 lut 20:19
Mila:
Oczywiście, to literówka.
ΔBED∼ΔBCA
6 lut 20:21
Michał: dziękuję a literówki się zdarzają ja tylko chciałem się upewnić
6 lut 21:16
 |BC|=a
|DC|=d√2
|BE|=a−d
d<a
ΔBED∼ΔBCE⇔
|BC|=a
|DC|=d√2
|BE|=a−d
d<a
ΔBED∼ΔBCE⇔