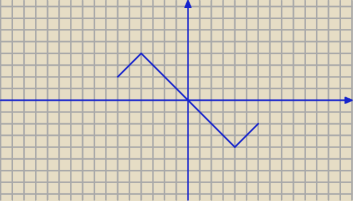
Na rysunku przedstawiono wykres funkcji. wojciech31: Na rysunku przedstawiono wykres funkcji f : <−6;6> → R. Ile punktów wspólnych z osią OX ma wykres funkcji g? g(x) = ||f(x)|−3|−1

blacky6: Wydaję mi się że nalezy przekształcić wykres funkcji wg następującego schematu Masz wykres f(x) 1 przekształcenie g(x)=|f(x)| odbicie wykresy leżącego pod osi OX 2. g(x)=|f(x)|−3 czyli przesunięcie o wektor [0,3] 3.g(x)= ||f(x)|−3| odbicie wykresy leżącego pod osi OX 4. g(x)=||f(x)|−3|−1 przesunięcie o wektor [0,1] Czyli musisz narysować 4 dodatkowe wykresy (przekształcić) i wtedy zobaczysz ile pinktów wspólnych będzie miał wykres. Jesli nie wiesz o co chodzi w przekształcenia wykresów to wpisz w google.

ucud: W punkcie 1. ten kawałek leżący w 4 ćwiartce mam "odbić" tak, żeby był w 1 ćwiartce?

Qulka: tak

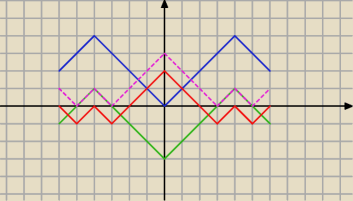
Qulka: 6 punktów

ucud: Dziękuję