 z.1
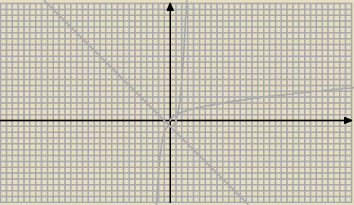
Dana funkcja nie jest ciągła w punktach x = 0 i x = 1
Powinna być określona, np.
− x − 1 dla x ≤ 0
f(x) = x3 − 1 dla 0 < x ≤ 1
√x dla x > 1
Wtedy będzie ciągła w ℛ .
z.1
Dana funkcja nie jest ciągła w punktach x = 0 i x = 1
Powinna być określona, np.
− x − 1 dla x ≤ 0
f(x) = x3 − 1 dla 0 < x ≤ 1
√x dla x > 1
Wtedy będzie ciągła w ℛ .
 z.2
f(x) = − x3 + 6 x2
a) Miejsca zerowe : 0 i −6
bo
− x3 + 6 x2 = 0
− x2*( x + 6) = 0
x = 0 lub x = − 6
==============
b) Pochodna
f'(x) = − 3 x2 + 12 x
f'(x) = 0 ⇔ − 3 x2 + 12 x = 0 ⇔ − 3 x*( x − 4) = 0 ⇔ x = 0 lub x = 4
c) f'(x) < 0 ⇔ − 3 x2 + 12 x < 0 ⇔ − 3 x *( x − 4) < 0
x1 = 0 x2 = 4 a = − 3 < 0
więc
− 3 x*( x − 4) < 0 ⇔ x ∊ ( − ∞; 0) ∪ ( 4; + ∞ )
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
f'(x) > 0 ⇔ − 3 x*( x − 4) > 0 ⇔ x ∊ ( 0 ; 4)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
d) Ekstrema funkcji
W punkcie x 1 = 0 funkcja f' zmienia znak z − na + , więc w tym
punkcie funkcja f ma minimum lokalne ymin = f(0) = 0
−−−−−−−−−−
W punkcie x2 = 4 funkcja f' zmienia znak z + na −, więc w tym
punkcie funkcja f ma maksimum lokalne ymax = f(4) = − 43 + 6*42 = − 64 + 6*16 =
= − 64 + 96 = 32
−−−−−−−−−−
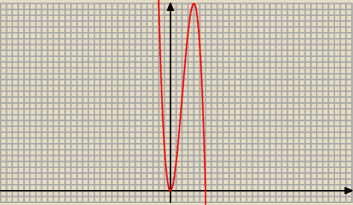
Patrz na wykres funkcji f :
z.2
f(x) = − x3 + 6 x2
a) Miejsca zerowe : 0 i −6
bo
− x3 + 6 x2 = 0
− x2*( x + 6) = 0
x = 0 lub x = − 6
==============
b) Pochodna
f'(x) = − 3 x2 + 12 x
f'(x) = 0 ⇔ − 3 x2 + 12 x = 0 ⇔ − 3 x*( x − 4) = 0 ⇔ x = 0 lub x = 4
c) f'(x) < 0 ⇔ − 3 x2 + 12 x < 0 ⇔ − 3 x *( x − 4) < 0
x1 = 0 x2 = 4 a = − 3 < 0
więc
− 3 x*( x − 4) < 0 ⇔ x ∊ ( − ∞; 0) ∪ ( 4; + ∞ )
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
f'(x) > 0 ⇔ − 3 x*( x − 4) > 0 ⇔ x ∊ ( 0 ; 4)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
d) Ekstrema funkcji
W punkcie x 1 = 0 funkcja f' zmienia znak z − na + , więc w tym
punkcie funkcja f ma minimum lokalne ymin = f(0) = 0
−−−−−−−−−−
W punkcie x2 = 4 funkcja f' zmienia znak z + na −, więc w tym
punkcie funkcja f ma maksimum lokalne ymax = f(4) = − 43 + 6*42 = − 64 + 6*16 =
= − 64 + 96 = 32
−−−−−−−−−−
Patrz na wykres funkcji f :
 z.3
z.3
| 1 | ||
f(x) = | x3 + x2 + 5 określona jest na A = < − 1 ; 1 > | |
| 3 |
| 1 | 1 | 2 | ||||
f( − 1) = | *( −1)3 + (−1)2 + 5 = − | + 1 + 5 = 5 | ||||
| 3 | 3 | 3 |
| 1 | 1 | 1 | ||||
f(1) = | *13 + 12 + 5 = | + 1 + 5 = 6 | ||||
| 3 | 3 | 3 |
| 1 | ||
f '(x) = | *3 x2 + 2 x = x2 + 2 x = x*( x + 2) = 0 ⇔ x = 0 lub x = − 2 | |
| 3 |
| 5 | 1 | |||
Z tych trzech liczb : | {3}, 6 | , 5 wybieramy najmniejszą: | ||
| 2 | 3 |
| 1 | ||
fmax = 6 | ||
| 3 |
| 2 | 1 | |||
Z tych trzech liczb : 5 | , 6 | , 5 wybieramy najmniejszą : .... itd. | ||
| 3 | 3 |