styczna do okręgu przechodząca przez dany punkt Kinga: witam, proszę bardzo o pomoc w takim zadaniu: napisz równanie ogólne stycznych do danego okręgu o i przechodzących przez punkt A, jeśli o: x²+y²−6x+8y+21=0, A(5,−1) ja liczyłam to w ten sposób 5a+b=−1, czyli b=−1−5a, stąd równanie ogólne ax−y−5a−1=0, następnie podstawiłam do wzoru na odległosć punktu od prostej (odległosc−promien koła, punkt−jego środek) niestety wyszło mi tylko jedno równanie, czyli 5x−12y −37=0, a powinno wyjśc jeszcze x−5=0, czy ktoś mógłby wymyslić bardziej uniwersalne rozwiązanie, które obejmuje te dwa wyniki?

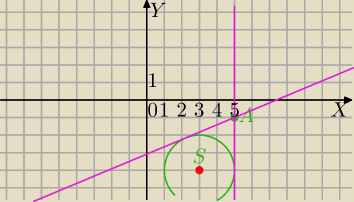
Mila: x²+y²−6x+8y+21=0, (x−3)²−9+(y+4)²−16+21=0 (x−3)²+(y+4)²=4 S=(3,−4), r=2 W przypadku , gdy korzystasz z równania prostej w postaci kierunkowej drugą styczną odczytujesz z rysunku. x=5 Albo Korzystasz z postaci ogólnej równania prostej: (*) Ax+By+C=0 A*5−B+C=0⇔C=B−5A (**) Ax+By+B−5A=0

	|3A−4B+B−5A|
		=2 po przekształceniach:
	√A2+B2

5B²+12AB=0 ⇔B(5B+12A)=0

	−12
B=0 lub B=		A
	5

Podstawiam do (**)

	12		12
Ax+0*y+0−5A=0 lub Ax−		Ay−		A−5A=0 /:A⇔
	5		5

	12		12
Ax−5A=0 /:A lub x−		y−		−5=0 /*5⇔
	5		5

x−5=0 lub 5x−12y−37=0

Kinga: o, dziękuję już rozumiem