qwqwq hennio: Ramiona trójkata mają długość 3 i 7,a kąt między nimi 120*.Wyznacz długość odcinka dwusiecznej kąta rozwartego zawartego w trójkącie.

Mila:

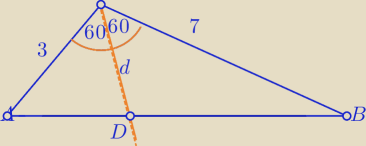
	1		21		21		√3
PΔABC=		*3*7*sin(120o)=		*sin(60)=		*
	2		2		2		2

	21√3
PΔABC=
	4

	1		1		3d*√3		7d*√3
PΔABC=		*3*d*sin(60o)+		*7*d*sin(60o)=		+
	2		2		4		4

⇔

21√3		10d*√3
	=		⇔
4		4

	21
d=
	10

=======

Mila:

hennio: dzięks

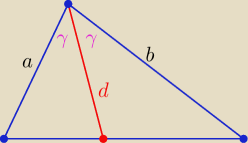Eta: Wykaż,że w trójkącie długość odcinka "d" zawartego w dwusiecznej kąta

	2ab
między bokami a i b wyraża się wzorem d=		*cosγ
	a+b

	2*3*7		21
to w tym zadaniu : d=		*cos60o =
	3+7		10