Pochodne
Czarek: Zbadaj istnienie pochodnej funkcji f = |x|x2 w punkcie x = 0.
6 lut 15:21
Dziadek Mróz:
f(x) = |x| * x
2
|x| * |x| = |x
2| = x
2 bo x
2 ≥ 0
| | x3 | |
f'(x) = [|x| * x2]' = [|x|]' * x2 + |x| * [x2]' = |
| + 2x|x| = |
| | |x| | |
| | x3 | | 2x3 | | 3x3 | |
= |
| + |
| = |
| |
| | |x| | | |x| | | |x| | |
D :
|x| ≠ 0
x ≠ 0
D : {x ∊ ℛ : x ≠ 0}
Nie istnieje pochodna w punkcie x = 0.
6 lut 15:33
Gray: Z definicji pokaż, że f'(0)=0,
6 lut 16:44
Mila:
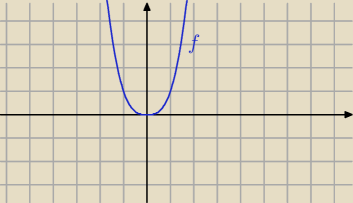
6 lut 17:11
