różne Anna: Proszę o sprawdzenie 2 zadań i pomocy/podpowiedzi w 2 innych zadaniach. 1)

	1
Wyznacz wszystkie wartości parametru k, k∊R, dla których równanie (cosx+		)(sinx−k)=0 ma
	2

trzy rożne rozwiązania w przedziale <0, 2π>.

	1
cosx=−
	2

	2		4
x=		π v x=		π
	3		3

2 różne rozwiązania sinx=k 1 rozwiązanie dla k=1 v k= −1 czyli odp: k∊{−1, 1} 2) Wyznacz wartości parametru p, dla których dziedziną funkcji f(x) = √(p3 + 2p2 − p − 2)x + 1 −3p jest zbiór liczb rzeczywistych. a=0 i 1−3p≥0

	1
(p3 + 2p2 − p − 2) = (p − 1)(p + 1)(p + 2) i p ≤
	3

p∊{−2, −1} 3) Na trapezie można opisać okrąg, można w ten trapez także wpisać okrąg. Oblicz promienie tych okręgów, jeśli podstawy mają długość 4 i 16. skoro można na tym trapezie opisać i wpisać okrąg, to jest on równoramienny, czyli ramiona mają 10 obliczyłam promień okręgu wpisanego r=4 ale nie mam pojęcia jak obliczyć promień okręgu opisanego R 4) Wyznacz zbiór wartości funkcji f(x) = x² + | log₂₀₁₄x |* log_x2014

	1
logx2014 =
	log2014x

	| log2014x |
f(x)= x2 +		=x2 + |1|
	log2014x

czyli

	⎧	x2 + 1 , gdy log2014x ≥0
f(x)	⎩	x2 − 1 , gdy log2014x <0

to jest dobrze? czyli to znaczy, że Zw=(−∞; −1> ∪ <1; +∞) ?

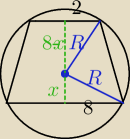
Qulka: x²+8²=R² (8−x)²+2²=R²

J: zad 4) zastanów się nad dziedziną tej funkcji

Qulka: w 4 na dzień dobry x>0 bo to liczba logarytmowana błąd w zapisie bo |1| to 1 analiza dalej poprawna ..wniosek nie ZW te niebieskie kawałki

J: x = 1 też nie należy do dziedziny...

Anna: czyli powinno być x² +1, gdy log₂₀₁₄x > 1 x² −1, gdy log₂₀₁₄x ∊(0;1) ? czy wcześniej miałam dobrze? ZW ∊(−1;0)∪(2;+∞)

Qulka: też nie tam powinny być wszędzie kółeczka..ale tyle razy poprawiałam niebieskie że już byłam zmęczona

Qulka: wcześniej miałaś dobrze log a efektem rozwiązania będą same x w tych przedziałach co napisałaś niżej

J: Rozwiązanie: 14:26 prawidłowe

Anna: czyli x² +1, gdy log₂₀₁₄x ≥0 , x>1 x² −1, gdy log₂₀₁₄x <0 , x∊(0;1)

Qulka: czyli ⎧ x2 + 1 , gdy log2014x ≥0 f(x) ⎩ x2 − 1 , gdy log2014x <0 więc x2 +1, gdy x > 1 x2 −1, gdy x ∊(0;1) ? ZW ∊(−1;0)∪(2;+∞)

Qulka: o właśnie

Anna: Ok : ) Dziękuję bardzo : ) a pozostałe zadanka?

J: zad 1) OK

Anna: w zadaniu 2) widzę, że "zjadłam" potęgi, powinno być: 2) Wyznacz wartości parametru p, dla których dziedziną funkcji f(x) = √(p³ + 2p² − p − 2)x + 1−3p jest zbiór liczb rzeczywistych. a=0 i 1−3p≥0

	1
(p3 + 2p2 − p − 2) = (p − 1)(p + 1)(p + 2) i p ≤
	3

p∊{−2, −1}

Qulka: ok

Anna: Dziękuję bardzo za pomoc i sprawdzenie zadanek : )

Qulka: z co Ci wyszło w 3?

Anna:

5√41
4

Qulka: wygląda ok

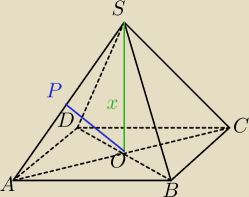
Anna: mam jeszcze takie zadanie: W ostrosłupie prawidłowym czworokątnym odległość środka podstawy ostrosłupa od jego krawędzi bocznej wynosi √3. a) Wyznacz objętość V ostrosłupa jako funkcję jego wysokości x i podaj dziedzinę tej funkcji b) Dla jakiej wartości x objętość ostrosłupa jest najmniejsza? Oblicz tę objętość. c) Naszkicuj wykres funkcji V hym, nie wiem czy dobrze, ale wyszło mi

	2x2√3
a) V(x)=
	3√x2−3

D: x∊(√3; +∞) b) dla x=√6 V(√6)=4 c) nie wiem czy da się jakoś na skróty zrobić, więc chyba trzeba zrobić przebieg zmienności funkcji...

andrzejh: halo

halo: halo

Filip: |PS| = √x² − 3

√x2 − 3		2x
	=
x		a√2

	√2x2
a =
	√x2 − 3