zad. 6 Udowodnij, że dla dowolnych liczb rzeczywistych a i b 10a2−6a−2ab+b2+2>0
http://i61.tinypic.com/4v01ao.jpg
zad.17 Ze zbioru cyfr {1,2,3,4,5,6,7,8,9} tworzymy liczby pięciocyfrowe o różnych cyfrach i
spośród nich wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo wylosowania liczby,
której suma cyfr jest nieparzysta.
Niby wynik mi tutaj wyszedł dobry, ale nie jestem pewna, czy ja to dobrze rozpisałam...
http://i57.tinypic.com/23r269y.jpg
I mam jeszcze problem z tym zadaniem:
Przekątne trapezu dzielą go na cztery trójkąty. Pola trójkątów zawierających podstawy trapezu
są równe odpowiednio m2 i n2. Udowodnij, że pole trapezu jest równe (m+n)2.
A więc wiem, że te dwa kolejne trójkąty będą miały pole po m*n, próbowałam rozwiązać,
oznaczając wysokość jednego trójkąta przez h1, drugiego przez h2, podstawy przez a i b i z
różnych równań coś wykombinować, jednak nic konkretnego mi nie wyszło :C
Proszę o pomoc 
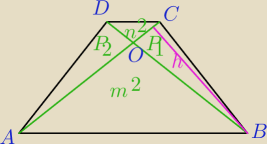1) ΔDOC∼ΔAOB cecha kkk
| PΔDOC | n2 | |||
2) | = | ⇔ | ||
| PΔAOB | m2 |
| n | ||
ΔDOC∼ΔAOB w skali k= | ||
| m |
| OC | n | |||
3) | = | |||
| OA | m |
| PΔCOB | n | n | |||
= | ⇔PΔCOB= | *m2=m*n | |||
| P ΔBOC | m | m |
Bardzo proszę
Dziękuję
