Oblicz obów i pole koła wpisanego w trójkąt prostokątny

Oblicz obów i pole koła wpisanego w trójkąt prostokątny xfgsy: Oblicz pole i obwód koła wpisanego w trójkąt prostokątny o przyprostokątnych 6 i 4. Najlepiej gdyby udało się skorzystać z któregoś z tych wzorów na pola trójkątów P= ¹₂ *ah (równoramienny) P= ^{a √3}₄ (równoboczny) P=¹₂ * ab (prostokątny) P= ¹₂ absinα (różnoramienny) P= √p(p−a)(p−b)(p−c) (Herona) P= p*r (wpisany)

	abc
P=		(opisany)
	4R

Proszę o szczegółowe wyjaśnienie co z czego się wzięło. Dziękuje emotka

6 lut 00:03

Qulka: trójkąt prostokątny oparty jest na średnicy , więc z pitagorasa policz przeciwprostokątną i podziel ją na dwa to będzie promień potem wzór na pole koła i obwód emotka

6 lut 00:05

Qulka: wróć ...on ma być wpisany emotka

to wzór przedostatni..więc przeciwprostokątna i tak Ci potrzebna

6 lut 00:06

Qulka: P_Δ = 6•4/2=12 połowa obwodu Δ czyli p = 5 + √13

	12
r=
	5 + √13

6 lut 00:08

xfgsy: @Qulka nic z tego nie rozumiem co napisałaś emotka

6 lut 00:12

Eta:

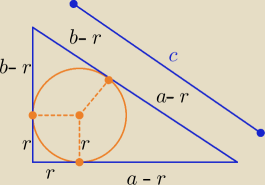
c= a−r+b−r ⇒ 2r= a+b−c ⇒ r=... P=πr²=... L= 2πr=....

6 lut 00:15

xfgsy: Potrafi to ktoś wytłumaczyć KROK PO KROKU ? Wszystko dokładnie..

6 lut 00:26

pigor: ..., np. tak : P_Δ=¹₂*6*4= 3*4=12 − pole Δ ; a=6, b=4 ⇒ c²= 6²+4²= 36+16= 52= 4*13 ⇒ c=2√13 ⇒ ⇒ połowa obwodu Δ : p= ¹₂(a+b+c)= ¹₂(6+4+2√13)= 5+√13 zatem z wzoru na pole Δ P=pr , gdzie r − dł. promienia okręgu wpisanego w Δ ⇒

	P		12		12(5−√13)		12(5−√13)
⇒r=		=		=		=		=5−√13
	p		5+√13		25−13		12

P_k=π r²=π(5−√13)²=(25−10√13+13)π=(38−10√13)π=2(19−5√13)π O_k= 2πr= 2π(5−√13) − szukany obwód . ... emotka

6 lut 00:32

xfgsy: Chyba zrozumiałam, dzięki emotka

6 lut 15:20