Zbadać monotoniczność Marcin: Zbadać monotoniczność i znaleźć ekstrema funkcji.

	4
f(x) = x +
	x

Proszę o pomoc. Dobrze rozumiem, że trzeba zacząć od policzenia pochodnej? Czyli:

	4
f'(x) = 1 −		(prawidłowo ją w ogóle policzyłem?)
	x2

Saris: 1. Dziedzina 2. Pochodna 3. Sprawdzić gdzie pochodna się zeruje (ekstremum) gdzie jest dodatnia (rośnie) gdzie ujemna (maleje).

Marcin: 1. Dziedzina − czyli wychodzi "x" należy R / {0} ? 2. Pochodna − tak jak napisałem wyżej (prosiłbym potwierdzić, czy dobrze ją policzyłem, jeżeli nie, to prosze o wskazanie błędu)

john2: Tak i tak.

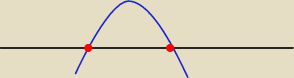
Marcin: Idąc dalej: otrzymaną pochodną przyrównuję do 0. Wychodzi mi, że "x=2" lub "x=−2" Następnie szkicuję wykres: Funkcja rośnie: x należy (−2;2) Funkcja maleje: x należy od (− nieskończności; 2) ; (2; + nieskończoności) Zgadza się?

john2: dlaczego Twoja parabola ma ramiona w dół skierowane?

Marcin: Fakt, powinny być skierowane do góry. Czyli będzie rośnie: : x należy od (− nieskończności; − 2) ; (2; + nieskończoności) maleje: x należy od (−2;2)

john2: Nie uwzględniłeś dziedziny jeszcze.

Marcin: To znaczy? W którym momencie mam ją uwzględnić? Przepraszam za nieco banalne pytania, ale dawno nie robiłem tego typu zadań i trochę się gubię.

john2: napisałeś, że funkcja maleje w przedziale (−2,2), co nie jest prawdą, bo w x = 0 nie ma funkcji, więc nie może tam maleć, funkcja maleje w przedziale (−2,0)u(0,2)