zadanie
Blue: Czworościan foremny o krawędzi a przecięto płaszczyzną równoległą do dwóch przeciwległych
krawędzi. Wyznacz pole otrzymanego przekroju będącego wielokątem jako funkcję długości odcinka
wyznaczonego przez ten przekrój na jednej z pozostałych krawędzi. Zbadaj przedziały
monotoniczności i ekstrema funkcji.
Mógłby ktoś zrobić rysunek? Może jakaś podpowiedź ?
5 lut 16:49
Tadeusz:
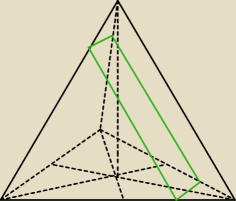
5 lut 18:52
Blue: To który przekrój jest poprawny? Mili czy Tadeusza?
5 lut 19:11
Tadeusz:
... każda pliszka swój ogonek chwali −
5 lut 19:44
Tadeusz:
... krawędzie przeciwległe czworościanu to takie które nie mają wspólnego wierzchołka
(każda z krawędzi w nim ma tylko jedną przeciwległą)
Na Jej rysunku przeciwległe są np AC i SB
5 lut 19:48
Blue: ale te krawędzie nie są równoległe... więc jak ten przekrój może być równoległy równocześnie do
dwóch krawędzi?
5 lut 20:28
Tadeusz:
... to musisz długo na to popatrzyć−
5 lut 20:31
Tadeusz:
Odpowiedz sobie na pytanie o prostą równoległą do płaszczyzny
5 lut 20:33
Blue: Tadeusz mógłbyś to wytłumaczyć, bo nie rozumiem... wybacz
5 lut 20:40
5 lut 20:52
Kacper:
5 lut 20:58
Tadeusz:
Proste by być równoległe do płaszczyzny nie mogą mieć z nią punktu stycznego
(i tylko tyle) Wzajemnie równoległe być nie muszą −
ba ... mogą być do siebie prostopadłe leżąc na jednej płaszczyźnie a jednocześnie być
równoległe do innej płaszczyzny −
5 lut 21:01
Blue: Dobrze... a zatem apeluję: mógłby ktoś całe to zadanie omówić, bo chyba nie dam rady go sama
rozwiązać ?
5 lut 21:06
Tadeusz:
... a co tu jest jeszcze do omawiania?
Jeśli wybierzesz dowolną krawędź czworościanu to ma ona tylko jedną przeciwległą.
Teraz masz przekroić czworościan płaszczyzną równoległą jednocześnie do obu tych
krawędzi. Płaszczyzn takich można znaleźć nieskończenie wiele ...
(różna odległość krawędzi od płaszczyzny) W zależności od tej odległości zmieniać się będzie
pole przekroju.
W zadaniu oczekują abyś to pole wyraziła funkcją długości odcinka jaki odłożyła płaszczyzna
na jednej z pozostałych krawędzi.
5 lut 21:19
Tadeusz:
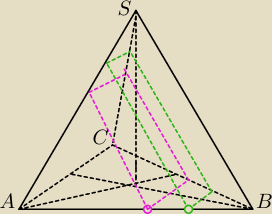
5 lut 21:31
Tadeusz:
i jak zwykle... okręciła się na pięcie ... i bawcie się dalej sami −
5 lut 21:48
Blue: Już jestem Tadeusz, nie obrażaj się
5 lut 22:09
Blue: A mógłbyś mi pokazać ten odcinek, którym mam wyrazić to pole
5 lut 22:11
Tadeusz:
... a widzisz te punkty ... zielony ... liliowy −
5 lut 22:17
Tadeusz:
... to jest bardzo "przekrojowe" zadanko ...i geometria w przestrzeni i badanie funkcji
Na maturę chyba nazbyt "czasochłonne" ale kto wie ... −
5 lut 22:20
Blue: Czyli ten odcinek jest od tej różowej kropki do zielonej?
5 lut 22:25
Tadeusz:
... Ty chyba już śpisz −
5 lut 22:27
Blue: No właśnie mam zamiar iść spać...
5 lut 22:29
Tadeusz:
Jeśli płaszczyzna ma przecinać czworościan (nie musi) to ten punkt będzie przemieszczał się
od B do A (zielone ... liliowe to przykładowe położenia)
5 lut 22:29
Blue: W ogóle Tadeusz, to po co Ty narysowałeś dwa przekroje?
5 lut 22:30
Blue: Czyli ten odcinek to np. od różowej kropki do A albo B albo od zielonej kropki do A albo B..?
5 lut 22:32
Blue: Bobra, idę spać, zajrzę jutro, może ktoś pokaże całe rozwiązanie
5 lut 22:35
Tadeusz:
... i teraz odpowiedz mi proszę: jeśli odcinek od B do zielonego punktu jest x
to jakie wymiary ma przekrój
? (zielona przerywana)
5 lut 22:35
Tadeusz:
trudno się z Tobą pracuje bo Ty nie czytasz tego co się do Ciebie pisze
Przeczytaj co napisałem o 21:19
Takich płaszczyzn jest nieskończenie wiele ... pokazałem dwie przykładowe
5 lut 22:37
Tadeusz:
... jak się wyśpi ... to zakuma ... niebieska żabcia −
5 lut 23:17
Mila:
Cześć Tadeusz , masz rację, z rysunkiem, mój było innej treści. Nie zaskoczyłam, że to
chodzi o skośne krawędzie.
Pozdrawiam .
Często Blue nie przyjmuje do wiadomości uwag i upiera się przy swoim.
5 lut 23:31
Tadeusz:
witalski−
5 lut 23:33
Blue: Już rozumiem Tadeusz , będzie P = (a−x) * x, gdzie x to ten odcinek
ale nie rozumiem czegoś co jest w odpowiedziach:
min = 0 , ale przecież pochodna to będzie funkcja liniowa, więc dlaczego jest i minimum i
maximum?
6 lut 12:03
Tadeusz:
... fajnie −
ale jak widzę nie całkiem rozumiesz −
Zadanie o rozpatrujesz w określonym przedziale −
6 lut 12:13
Tadeusz:
wyobraź sobie przypadki gdy x=0 lub x=a
6 lut 12:17
Tadeusz:
... no i mylisz ekstremum ... z wartością minimalną w przedziale −
6 lut 12:34
Blue: Mógłby ktoś rozpisać to zadanie?
6 lut 23:32
Tadeusz:
słuchaj "żabko" niebieska −
Przecież wszystko masz już pod kontrolą
P=x(a−x) i sama to napisałaś
Masz funkcję kwadratową ... po kie licho Ci tu pochodna.
Wierzchołek znasz, przedziałów monotoniczności nie napiszesz?
Czego jeszcze brakuje? −
7 lut 00:04
Blue: a więc wcale nie trzeba korzystać z pochodnej
Ja jak widzę ekstrema, to zaraz bym pochodną
liczyła
7 lut 09:21
Blue: Dzięki Tadeusz
7 lut 09:21
===:
pochodną też możesz ...tylko przy funkcji kwadratowej to troszkę dłuższa ścieżka −
7 lut 10:55