5 lut 09:07
Hugo: [0 * arctg(1/0)] = [0 * arctg(oo)] = 0 * 0 = 0

5 lut 09:10
kyrtap: | | | |
ale limx→0− |
| już nie  |
| | | |
5 lut 09:11
Hugo: w zasadzie

[0 * arctg(1/0)] = [0 * arctg(−oo)] = 0 * (π − arctg(0) ) = 0 * p/2 = 0
arctg(−x) = π − arctg(x)
5 lut 09:15
Hugo: tam jest ARC CTG


5 lut 09:15
Eve: znowu obaj mieszacie

5 lut 09:17
Hugo: To jak w koncu

5 lut 09:17
Eve: czekaj policzę sposobem drugim
5 lut 09:20
Hugo: 3/ Extemum funkcji f = e
xsinx w przedziale −π<x<π
pochodna
f '= e
xsinx + e
xcosx
0 = e
xsinx + e
xcosx /dzielimy przez e
x Das to przete dodatnie

sinx = −cosx

5 lut 09:22
Hugo:
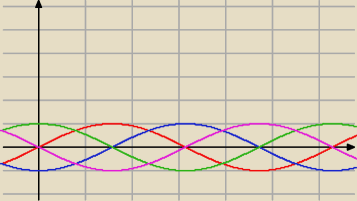
5 lut 09:24
Hugo: kiedy sinx + cosx daje zero

5 lut 09:24
Eve: tak czy siak, granica = 0 i pierwszy sposób też jest ok
5 lut 09:24
Hugo:
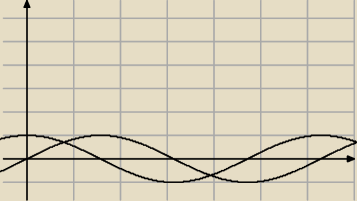
sinx = − cosx /
2
sin
2x = cos
2x
sin
2x = 1 − sin
2x
2 sin
2x = 1
sin
2x = 1/2
5 lut 09:27
Hugo: tam nie dawalem ze jest minus nie skonczonosc

wiec moglby obciąć
5 lut 09:28
Eve: tera ok
5 lut 09:29
Hugo:
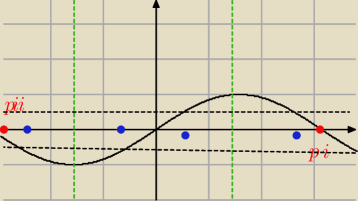
5 lut 09:33
Hugo: 4 rozwiązania
x = pi/4 v x = −pi/4 v pi −pi/4 v −pi + pi/4
5 lut 09:34
Hugo: całki ∫ x
√x2−1 dx
podstawianie czy części

? podstawiani !
t = x
2 − 1
dt = 2x dx
dt/2 = x dx
∫
√t dt/2


5 lut 09:41
Hugo: b)
∫ xln(x+1) dx
przez części
u = ln(x+1)
v' = x
v = x
2/2
| | 1 | |
ln(x+1) * x2/2 − ∫ |
| * x2/2 dx |
| | 1+x | |
| | x2 | |
ln(x+1) * x2/2 − 0,5∫ |
| * dx |
| | 1+x | |
| | x2−1 + 1 | |
ln(x+1) * x2/2 − 0,5∫ |
| * dx |
| | 1+x | |
| | x2−1 | | 1 | |
ln(x+1) * x2/2 − 0,5∫ |
| dx − 0,5∫ |
| dx |
| | 1+x | | 1+x | |
ln(x+1) * x
2/2 − 0,5∫ (x+ 1)dx − 0,5ln(1+x) + C
ln(x+1) * x
2/2 − 0,5( x
2/2 + x) − 0,5ln(1+x) + C
5 lut 10:00
Eve: ok
5 lut 10:06
Eve:
∫
√ex−1dx=
| | dt | |
ex−1=t, ex=t+1, exdx=dt, dx= |
| |
| | t+1 | |
5 lut 10:13
bezendu:
Kobiety, Hugo, Taniec, Śpiew

5 lut 10:19
Eve: 
5 lut 10:31
Hugo: 
5 lut 10:38
Hugo: SUCHAR Z ALGEBRY
.
.
.
.
.
Ciekawi cie jaki?
.
.
.
.
.
.
myslisz ze jest dobry ?
.
.
.
.
.
zaraz padniesz

.
.
.
.
jeszcze za chwile.
.
.
.
Dopiero kiedy poszedłem na studia, zrozumiałem pytanie tak często zadawane w dzieciństwie:
czaisz bazę?
5 lut 10:39
Eve: 
5 lut 10:40
Hugo: orgasm

5 lut 10:44
bezendu:
Eva żałuj, że nie przeczytałaś pasty o krasnoludzie

5 lut 10:51
Hugo: Hugo ten przyklad sam
∫
√ex −1dx
t = e
x − 1 −−−> e
x = t + 1
dt = e
x dx
dx = dt/e
x
dx = dt/t + 1 podstawiamy do tego ∫
√ex −1dx
| | dt | | √t | |
∫ √t |
| = ∫ |
| dt |
| | t+1 | | t+1 | |
części?
5 lut 11:04
Hugo:
u =
√t
v = ln|t+1| ?
mam wrazenie ze błądze
| | 1 | |
√tln|t+1| − ∫ |
| ln|t+1| dt |
| | 2√t | |
5 lut 11:07
Eve:
v'=
√t, v=2
√t
| | √t | | √t | |
∫ |
| dt=2√tln(t+1)−2∫ |
| |
| | t+1 | | t+1 | |
przenieś całkę na lewo
5 lut 11:25
Eve: cos mi nie poszło

5 lut 11:27
razor: | | √t | | u*2udu | | 2u2 | |
∫ |
| dt = | u = √t, u2 = t, 2udu = dt| = ∫ |
| = ∫ |
| du = |
| | t+1 | | u2+1 | | u2+1 | |
| | 2(u2+1)−2 | | 1 | |
∫ |
| du = ∫2du − 2∫ |
| du = 2u − 2arctgu = 2√t − 2arctg√t + C |
| | u2+1 | | u2+1 | |
5 lut 11:38
Hugo: 
nikt tego nie umie, nie przejmuj sie. ZALICZE TO USTANIE !
u =
√t
u
2 = t
2u du = dt
∫ ln|u
2+1| du
nie ma wzoru na ln

wiec przez części?
y = ln|u
2+1|
v' = 1
v = u
| | 1 | |
ln|u2+1|* x − ∫ |
| * 2u * du |
| | u2+1 | |
| | 2u | |
ln|u2+1|* x − ∫ |
| du |
| | u2+1 | |
5 lut 11:45
Eve: a ja kombinowałam z całka z ln

5 lut 11:45
Hugo: RAZOR

mamy to samo tylko ze Hugo zapisal pare naście wierszy więcej

5 lut 11:47
Hugo: easy

mamy prawie 12 −> 14 egzamin
to przyblizenie cza

5 lut 11:47
bezendu:
Hugo taki zdolny i egzamin ?

5 lut 11:48
Hugo: moge napisac z cb bezendu w przyszlym semestrze za tego browca bo nie pilem

5 lut 11:52
5 lut 12:16
Hugo: cos(pi/2) ~ 1 −x2/8 dla |x|<0,1
f(x) = cos(x/2)
f'(x) = −sin(x/2) * 0,5
f''(x) = −cos(x/2) * 0,5 * 0,5
f'''(x) = sin(x/2) * 0,5 0,5 * 0,5
f''''(x) = f(x) = cos(x/2) * 0,5 0,5 * 0,5 * 0,5
5 lut 12:19
Hugo: f(0) = 1 * 0,5
f'(0) = 0
f''(0) = −1 * 0,5 * 0,5
f'''(0) = 0
f''''(0) = 1 * 0,5 * 0,5 * 0,5
5 lut 12:23
5 lut 12:28
Hugo: cos(x/2) = f(0) − x2/2! + cos(c/2)x4/4!
5 lut 12:28
 poza przyblizeniami
http://www.isimiip.agh.edu.pl/wiki/doku.php/1/zima/analiza/egzaminy/2014/termin0
1.lim x−>0− x3arcctg(1/x) oblicz granice
poza przyblizeniami
http://www.isimiip.agh.edu.pl/wiki/doku.php/1/zima/analiza/egzaminy/2014/termin0
1.lim x−>0− x3arcctg(1/x) oblicz granice


 [0 * arctg(1/0)] = [0 * arctg(−oo)] = 0 * (π − arctg(0) ) = 0 * p/2 = 0
arctg(−x) = π − arctg(x)
[0 * arctg(1/0)] = [0 * arctg(−oo)] = 0 * (π − arctg(0) ) = 0 * p/2 = 0
arctg(−x) = π − arctg(x)




 sinx = −cosx
sinx = −cosx 


 sinx = − cosx / 2
sin2x = cos2x
sin2x = 1 − sin2x
2 sin2x = 1
sin2x = 1/2
sinx = − cosx / 2
sin2x = cos2x
sin2x = 1 − sin2x
2 sin2x = 1
sin2x = 1/2
 wiec moglby obciąć
wiec moglby obciąć

 ? podstawiani !
t = x2 − 1
dt = 2x dx
dt/2 = x dx
∫ √t dt/2
? podstawiani !
t = x2 − 1
dt = 2x dx
dt/2 = x dx
∫ √t dt/2





 .
.
.
.
jeszcze za chwile.
.
.
.
Dopiero kiedy poszedłem na studia, zrozumiałem pytanie tak często zadawane w dzieciństwie:
czaisz bazę?
.
.
.
.
jeszcze za chwile.
.
.
.
Dopiero kiedy poszedłem na studia, zrozumiałem pytanie tak często zadawane w dzieciństwie:
czaisz bazę?




 nikt tego nie umie, nie przejmuj sie. ZALICZE TO USTANIE !
nikt tego nie umie, nie przejmuj sie. ZALICZE TO USTANIE !
 wiec przez części?
y = ln|u2+1|
wiec przez części?
y = ln|u2+1|

 mamy to samo tylko ze Hugo zapisal pare naście wierszy więcej
mamy to samo tylko ze Hugo zapisal pare naście wierszy więcej 
 mamy prawie 12 −> 14 egzamin
to przyblizenie cza
mamy prawie 12 −> 14 egzamin
to przyblizenie cza 

