R3 i nie tylko Lukas: Oblicz najmniejszą odelgłość między krzywymi 4x²+y²+32x+63=0 oraz x²+y²−x=0 Jak się wgl za to zabrać?

Gray: Czy to są krzywe? Nie wiem o co chodzi z tym "R³" w temacie. Jeżeli to jest w R³ to to nie są krzywe, tylko powierzchnie. W R² to są krzywe.

Lukas: Takie mam polecenie. Jutro mam egzamin i robię przykładowe zadania. Ale nie wiem wgl jak, pomożesz ?

Lukas: ?

Lukas: Pomoże ktoś ?

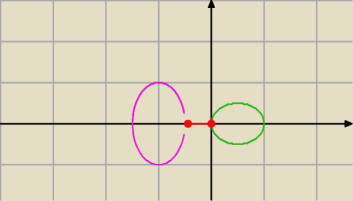
Gray: Najłatwiej to sobie narysować i odczytać tę odległość z wykresu. Pierwsza krzywa to; 4(x+4)²+y²=1, czyli elipsa (różowa na wykresie); druga to okrąg: (x−1/2)²+y²=1/4 (zielona). Odległość, to długość tego czerwonego odcinka.

Janek191: x² + y² − x = 0 ( x − 0,5)² − 0,25 + ( y − 0)² = 0 ( x − 0,5)² + ( y − 0) = 0,5² To jest okrąg o S = ( 0,5 ; 0) i r = 0,5 −−−−−−−−−−−−−−− Sprawdź jaką krzywą przedstawia I równanie

Lukas: Ale na egzaminie to muszę raczej policzyć ? a nie narysować

Lukas: Janek 191 elipsa jak napisał Grey. tylko mając teraz równanie elipsy 4(x+4)²+y²=1 nie trzeba tego dzielić przez 4

	y2		1
(x+4)2+		=		?
	4		4

Janek191: To wyznacz współrzędną lewej czerwonej kropki x₁ x₂ = 0 d = x₂ − x₁

Janek191: Jest to elipsa przesunięta o wektor [ − 4 ; 0 ]

( x + 4)2		y2
	+		= 1
1   4		1

Lukas: Janek a mógłbyś pokazać jak zrobić do konca bo ja już nie ograniam tego

Lukas: ?

Lukas: ?

J: ..oblicz współrzęne punktów przecięcia sie elipsy z osią OX i okręgu z osią OX

Lukas: Ale jak mam to obliczyć ? co podstawić ?

J: y = 0

Lukas:

	1
(x−0,25)2+0=		/ √
	4

	1
|x−0,25||=
	2

	1		1
x−0,25=		lub x−0,25=−
	2		2

	3		1
x=		lub x=−
	4		4

J: źle..

	1		1		1		1		1		1
(x −		)2 =		⇔ (x −		) =		lub (x −		) = −
	2		4		2		2		2		2

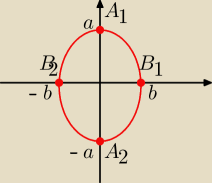
Janek191: Równanie elipsy , której środkiem jest punkt O = (0; 0) , a osiami są osie układu współrzędnych ma postać

x2		y2
	+		= 1
b2		a2

I A₁A₂ I = 2 a − długość osi wielkiej IB₁B₂ I = 2 b − długość osi małej Ogniska : F₁ = ( 0, c) F₂ = ( 0 , − c) oraz c² = a² − b² Mamy więc równanie

x2		y2
	+		= 1
1   ( )2   2		12

czyli

	1
b =		a= 1
	2

Po przesunięciu o wektor [ − 4; 0 ] otrzymamy

	1		1
b' =		− 4 = − 3
	2		2

zatem d = 0 − ( −3,5) = 3,5 ==================== Rysunek przedstawia elipsę

Lukas: dzieki

Janek191: Lub tak jako rzecze J : y = 0 więc

( x + 4)2
	+ 0 = 1
1     4

	1
( x + 4)2 =
	4

	1		1
x + 4 =		lub x + 4 = −
	2		2

x = − 3,5 lub x = − 4,5 Bierzemy x = − 3,5 ======= d = 0 − ( − 3,5) = 3,5 =====================

daras: ciekawe zadanie wymagające troszkę wyobraźni i pomyślenia ale z tym u studentów z pokolenia K&W krucho

daras: ale ciekawsze byłoby w ℛ³

Janek191: Co oznacza K&W ?

Janek191: Ja to odczytałem: kurwy i wino

Lukas:

daras: kopiuj i wklej