Błagam pomóżcie Radek: Czy mógłby mi ktoś pomóc. Bardzo proszę. Mam to zadanie an jutro a nie mam pojęcia jak się za nie zabrać W graniastosłupie trójkątnym prawidłowym długość krawędzi podstawy równa jest a. Odcinek łączący środki symetrii dwóch ścian bocznych widać ze środka ciężkości podstawy graniastosłupa pod kątem α. Oblicz objętość graniastosłupa.

BiebrzaFun :

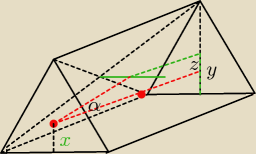
	1
x=		h
	3

	a√3		1		a√3		a√3
h=		⇒x==		*		=
	2		3		2		6

	1		1		a√3		a√3
y=		h=		*		=
	2		2		2		4

	a√3		a√3		a√3
z=y−x=		−		=
	4		6		12

	1
"od czerwonej kropki do czerwonej kropki"=		H ,gdzie H−wysokosć graniastosłupa
	2

	z		2z		a√3   2   12		a√3
tgα=		⇒H=		=		=
	1   H 2		tgα		tgα		6tgα

	a2√3		a√3		a3
V=		*		=
	4		6tgα		8tgα