Granice i miejsca zerowe Julia: Bardzo proszę o pomoc 1.− Podaj dziedzinę funkcji f(x)=2x³−x²−4x+2. Oblicz granicę funkcji na krańcach dziedziny. Wyznacz miejsca zerowe tej funkcji. 2.− Oblicz pochodną funkcji z punktu 1 f(x)=2x³−x²−4x+2 oraz wyznacz maxima i minima tej funkcji. Naszkicuj wykres. 3.− Oblicz pole obszaru ograniczonego okresem funkcji z punktu 1 f(x)=2x³−x²−4x+2 i osią x w zakresie od najmniejszego do największego miejsca zerowego tej funkcji. Jeśli nie udało Ci się wyznaczyć miejsc zerowych funkcji w punkcie 1, oblicz pole obszaru ograniczonego wykresem funkcji, osią x oraz prostymi o równaniach x=−1, x=1.

Janek191: z.1 Dziedziną każdego wielomianu jest zbiór liczb rzeczywistych ℛ. f(x) = 2 x³ − x² − 4 x + 2

	1		4		2
lim f(x) = lim x3*( 2 −		−		+		) = −∞*(2 − 0 − 0 + 0) = −∞
	x		x2		x3

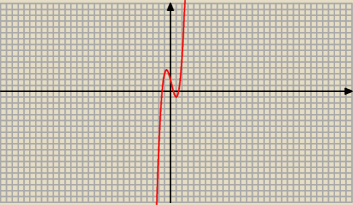
x→ −∞ x→ −∞ Podobnie lim f(x) = + ∞ x→+∞ Miejsca zerowe: f(x ) = x²*(2 x −1) − 2*( 2x −1) =(2 x −1)*( x² − 2) = (2 x −1)*( x −√2)*( x+ √2) = 0 ⇔ ⇔ x = − √2 lub x = 0,5 lub x = √2 Patrz − wykres danej funkcji:

J: 1. Naprawde nie potrafisz określić dziedziny? Jakie wartości może przyjmować zmienna x ? Miejsca zerowe: f(x) = ( x² −2 )(2x − 1) , zatem rozwiąż równanie: f(x) = ( x² −2 )(2x − 1) = 0

J: ..szkoda,że nie widziałem Twojego postu ....

Janek191: z.2 Pochodna funkcji f : f'(x) = 2*3 x² − 2 x − 4 = 6 x² − 2 x − 4 = 0 ⇔ 3 x² − x − 2 = 0 Δ = 1 − 4*3*(−2) = 25 √Δ = 5

	1 − 5		2		1 + 5
x =		= −		lub x =		= 1
	2*3		3		6

	2
W punkcie x = −		pochodna zmienia znak z + na − , więc
	3

	2
funkcja f osiąga wtedy maksimum lokalne ymax = f( −		) = ...
	3

W punkcie x = 1 pochodna zmienia znak z − na + , więc funkcja f osiąga wtedy minimum lokalne y_min = f(1) = − 1 II sposób: f'(x) = 6 x² − 2 x − 4

	2
f '(x) = 0 ⇔ x = −		lub x = 1
	3

Obliczam II pochodną : f''(x) = 12 x − 2 więc

	2		2		2
f''( −		) = 12*( −		) − 2 = − 8 − 2 = − 10 < 0 , więc w punkcie x = −
	3		3		3

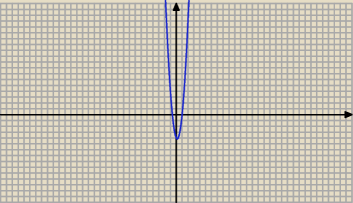
funkcja f osiąga maksimum lokalne. f''(1) = 12*1 − 2 = 10 > 0, więc w punkcie x = 1 funkcja f osiąga minimum lokalne. Na rysunku − wykres pochodnej ; y ' = 6 x² − 2 x − 4 Widać na nim jak funkcja pochodna zmienia znak. z + na − oraz z − na +.

Janek191: z.3 Ograniczone wykresem funkcji, a nie "okresem"

Janek191: Te zadania są ze szkoły ponadgimnazjalnej, czy ze studiów ?

Lukas: Janke pomożesz mi w moich postach ?

Janek191: Nic się nie odzywa, więc pewnie jest w szkole ?

Janek191: Co za Janke ? Może Jankes

Lukas: Janek191

Janek191: