trójkąt Kuba: W trójkąt równoramienny, w którym kąt między ramionami ma miarę 120 stopni wpisano okrąg o promieniu 6. Oblicz pole tego trójkąta.

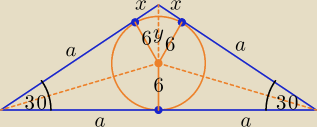
Bogdan: Propozycja rozwiązania: x√3 = 6 ⇒ x = 2√3, y = 2x = 4√3, a + x = 2(6 + y)

	1
Pole trójkąta P =		*(a + x)2*sin120o lub P = (2a + x)*6 lub P = a*(a + y)
	2

lub ... (jest jeszcze kilka innych sposobów na obliczenie pola tego trójkąta)

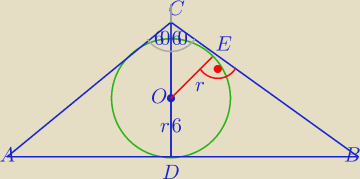
Mila: AB=a WΔCOE:

	r
sin60o=
	|OC|

√3		6
	=
2		|OC|

|OC|=4√3 |CE|=2√3 h=|CD|=6+4√3

	|DB|
tg60=
	h

	|DB|
√3=
	6+4√3

|DB|=6√3+12 P_Δ=(6√3+12)*(6+4√3) P_Δ=144+84√3 ==============