Pomożecie
ANia: Wykres funkcji kwadratowej f(x)=1/2x
2 przesunięto o cztery jednostki w prawo i otrzymano
wykres funkcji g(x). Wyznacz zbiór wszystkich argumentów x , dla których funkcja g(x)
przyjmuje wartości większe od 2


4 lut 18:47
pigor: ..., z warunków zadania :
f(x)= 12x2 →T
[4,0] → g(x)=
12(x−4)
2 i
g(x) >2 ⇔
⇔
12(x−4)
2 >2 /*2 ⇔ (x−4)
2 >4 ⇔ |x−4| >2 ⇔
⇔ x−4< −2 v x−4 >2 ⇔
x< 2 v x >6 ⇔
x∊(−∞;2) U (6;+∞).

4 lut 18:54
Janek191:
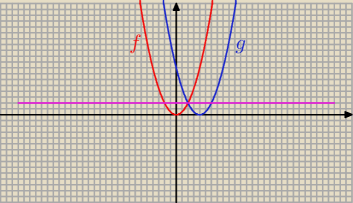
f(x) = 0,5 x
2
g(x) = 0,5( x − 4)
2
0,5( x − 4)
2 > 2
0,5 ( x
2 − 8 x + 16) > 2
0,5 x
2 − 4 x + 8 − 2 > 0
0,5 x
2 − 4 x + 6 > 0
Δ = 16 − 4*0,5*6 = 16 − 12 = 4
√Δ = 2
a = 0,5 > 0
więc
x ∊ ( −
∞ ; 2) ∪ ( 6 ; +
∞)
=====================
4 lut 18:57
Janek191:

f(x) = 0,5 x
2
g(x) = 0,5( x − 4)
2
0,5( x − 4)
2 > 2
0,5 ( x
2 − 8 x + 16) > 2
0,5 x
2 − 4 x + 8 − 2 > 0
0,5 x
2 − 4 x + 6 > 0
Δ = 16 − 4*0,5*6 = 16 − 12 = 4
√Δ = 2
a = 0,5 > 0
więc
x ∊ ( −
∞ ; 2) ∪ ( 6 ; +
∞)
=====================
4 lut 18:57
ANia: Dzięki wielkie

4 lut 18:59



 f(x) = 0,5 x2
g(x) = 0,5( x − 4)2
0,5( x − 4)2 > 2
0,5 ( x2 − 8 x + 16) > 2
0,5 x2 − 4 x + 8 − 2 > 0
0,5 x2 − 4 x + 6 > 0
Δ = 16 − 4*0,5*6 = 16 − 12 = 4 √Δ = 2
f(x) = 0,5 x2
g(x) = 0,5( x − 4)2
0,5( x − 4)2 > 2
0,5 ( x2 − 8 x + 16) > 2
0,5 x2 − 4 x + 8 − 2 > 0
0,5 x2 − 4 x + 6 > 0
Δ = 16 − 4*0,5*6 = 16 − 12 = 4 √Δ = 2
 f(x) = 0,5 x2
g(x) = 0,5( x − 4)2
0,5( x − 4)2 > 2
0,5 ( x2 − 8 x + 16) > 2
0,5 x2 − 4 x + 8 − 2 > 0
0,5 x2 − 4 x + 6 > 0
Δ = 16 − 4*0,5*6 = 16 − 12 = 4 √Δ = 2
f(x) = 0,5 x2
g(x) = 0,5( x − 4)2
0,5( x − 4)2 > 2
0,5 ( x2 − 8 x + 16) > 2
0,5 x2 − 4 x + 8 − 2 > 0
0,5 x2 − 4 x + 6 > 0
Δ = 16 − 4*0,5*6 = 16 − 12 = 4 √Δ = 2
