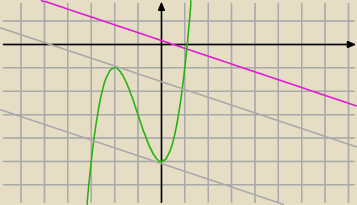
Znajdź równanie stycznej Siwy: Znajdź równanie stycznej do wykresu funkcji f(x)=x³+3x²−5 która jest równoległa do prostej: 2x+6y−1=0

Eve: oblicz pochodną i jej miejsca zerowe

Eve: inaczej styczna y=3x+b f'(x₀)=3)

Siwy: zrobiłem tak ale nie wiem czemu styczna wychodzi mi taka sama jak ta prosta i coś mi się nie zgadza z punktem styczności ?

Eve: jakie masz x₀?

Siwy: a dlaczego współczynnik wychodzi 3 ?

Siwy: bo mi wyszedł −1/3

Eve:

	1		1
2x+6y−1=0⇒y=−		x+
	3		6

Siwy: no tak więc współczynnik a1=a2=−1/3, gdyby była prostopadła to by było a=3

Tadeusz:

	1		1
2x+6y−1=0 ⇒ y=−		x+
	3		6

f(x)=x³+3x²−5

	1
f'(x)=3x2+6x 3xs3+6xs+		=0 ⇒ 9xs2+18xs+1=0
	3

policzysz punkty styczności a potem napiszesz równania stycznych

Eve: sorki, źle poczytałam

Siwy: zrobiłem dokładnie tak samo i ostatecznie prosta wychodzi mi y=/13*x+1/6?

Siwy: y=1/3*x+1/6

Siwy: f(x)=x3+3x2−5 2x+6y−1=0 y=−1/3*x+1/6 a=1/3 f'(x)=3x2+6x 3x²+6x+1/3=0 Δ=36−4=32 x1= −3−2√2/3 y1= 27 + 12√2/54 x2= −3+2√2/3 y2= 27 − 12√2/54 i potem wychodzi mi y=1/3*x+1/6 z y=ax+b ?

Siwy: czy ktoś może to rozwiązać od początku do końca?