 Dany jest ostrosłup prawidłowy trójkątny, którego pole powierzchni bocznej jest sześć razy
większe od pola podstawy. Oblicz sinus kąta, który krawędź boczna tworzy z podstawą.
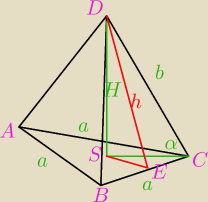
Pp − pole podstawy
Pb − pole boczne
Pśb − pole ściany bocznej
H − wysokość były
h − wysokość ściany bocznej
b − krawędź ściany bocznej
Dany jest ostrosłup prawidłowy trójkątny, którego pole powierzchni bocznej jest sześć razy
większe od pola podstawy. Oblicz sinus kąta, który krawędź boczna tworzy z podstawą.
Pp − pole podstawy
Pb − pole boczne
Pśb − pole ściany bocznej
H − wysokość były
h − wysokość ściany bocznej
b − krawędź ściany bocznej
| a2 √3 | 3a2 √3 | a2 √3 | 1 | |||||
Pp = | ⇒ Pb = | ⇒ Pśb = | = | a * h | ||||
| 4 | 2 | 2 | 2 |
| 2 | a √3 | |||
( | * | )2 + H2 = b2 | ||
| 3 | 2 |
| 1 | a √3 | |||
( | * | )2 + H2 = h2 | ||
| 3 | 2 |
| 1 | ||
( | a)2 + h2 = b2 | |
| 2 |
| a2 √3 | 1 | ||
= | a * h | ||
| 2 | 2 |