monotoniczność funkcji Ney: Przy okreslaniu przedzialow monotonicznosci funkcji kwadratowej spotykam sie, ze czasami jest to cos typu (−∞,p) a czasami (−∞,p> . Kiedy stosuje sie przedzial otwarty a kiedy zamkniety? Zawsze myslalem ze w funkcji kwadratowej zawsze jest przedzial domkniety przy wierzcholku.

J: logicznie rozumując przedziały powinny być otwarte ... trudno bowiem mówić o monotoniczności funkcji w punkcie ( wierzchołku) , tam jest ekstremum ..

Saris: Jeśli chodzi tylko o monotoniczność to jest kwestia umowy o ile pamiętam ^^.

Saris: Chociaż to co napisał J jest logiczne.

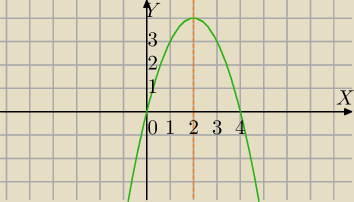
Mila: Jeśli masz sformułowanie "wyznacz maksymalne przedziały monotoniczności", to przedziały domknięte: np. f(x)=−x²+4 funkcja jest rosnąca w przedziale: (−∞,2>, malejąca w przedziale <2,∞). W innym przypadku tak jak radzi J.

Ney: O tym sfromulowaniu "maksymalne" to wiedzialem. Jednak robiac zadania i polecenie takie samo, tj. wyznacz przedzialy monotonicznosci a w odpowiedziach czasami otwarte, czasem domkniete.. Czyli mowicie ze zawsze dawac otwarte?

wmboczek: Jak można to pisz domknięte − wierzchołek spełnia definicję f(p)>f(p±α) lub f(p)<f(p±−α)

Ney: tylko w tym rzecz ze nie wiem kiedy mozna, a kiedy trzeba.

Gray: Jak funkcja jest ciągła, możesz domykać.

Ney: Ciagla tzn?