Parabola, prostokąt nawiększy obwód
que: Rozważmy prostokąty, których dwa wierzchołki leżą na osi OX, a pozostałe dwa mają
dodatnie rzędne i leżą na paraboli y = −x2 +6x. Oblicz obwód prostokąta o możliwie
największym polu.
3 lut 23:40
que: ?
3 lut 23:55
Qulka:
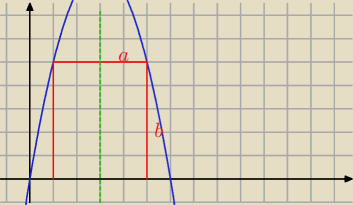
obwód prostokąta 4a +2b
pole 2a•b =2(x−3)•(−x
2+6x) = −2x
3+18x
2−36x i x∊(3,6)
max pole to ekstremum czyli pochodna =0
P' = −6x
2+36x−36 = 0
x
2−6x+6=0
delta.... x1 x2
4 lut 00:07
que: dzięki

4 lut 00:18
 obwód prostokąta 4a +2b
pole 2a•b =2(x−3)•(−x2+6x) = −2x3+18x2−36x i x∊(3,6)
max pole to ekstremum czyli pochodna =0
P' = −6x2+36x−36 = 0
x2−6x+6=0
delta.... x1 x2
obwód prostokąta 4a +2b
pole 2a•b =2(x−3)•(−x2+6x) = −2x3+18x2−36x i x∊(3,6)
max pole to ekstremum czyli pochodna =0
P' = −6x2+36x−36 = 0
x2−6x+6=0
delta.... x1 x2
