liczby zespolone + macierze taka sytuacja: Witam. chcę zaznaczyć, że proszę o rozwiązanie − Was to nic nie kosztuje, dla mnie jest to na wagę złota. Proszę o wyrozumiałość Były próby i różnego rodzaju metody, niestety nie daję rady. Jak napisałem wyżej, dla mnie jest to sprawa na wagę złota, czyli życia i śmierci jakby nie patrzeć − a zapewne Ciebie kosztuje tylko chwilę. Dlatego proszę o wyrozumiałość i bez zbędnych komentarzy. 1. Wyprowadź wzór na dzielenie liczb zespolonych w postaci algebraicznej w zbiorze liczb zespolonych rozwiązać równanie (wynik sprawdzić). 2. Omówić postać trygonometryczną liczby zespolonej. Obliczyc (wyniki pozostawić w postaci algebraicznej) 3. Podać definicję macierzy odwrotnej do macierzy stopnia n. Rozwiązać układ na dwa sposoby ( z tw. cramera oraz rozwiązując odpowiednie równanie macierzowe) 4.Podać definicję wyznacznika z macierzy kwadratowej A stopnia n. Obliczyć [URL=http://wstaw.org/w/3bDW/][IMG]http://wstaw.org/m/2015/02/03/unnamed_2_jpg_300x300_q85.jpg[/IMG][/URL] [url=http://wstaw.org/w/3bDR/][img]http://wstaw.org/m/2015/02/03/unnamed_1_jpg_300x300_q85.jpg[/img][/url]

taka sytuacja: http://wstaw.org/w/3bDW/ http://wstaw.org/w/3bDR/linki/ zdjęcia

Janek191: z.1 i² = − 1 a) ( − 1 + 3 i ) z² + ( 8 − 14 i) z − 11 + 23 i = 0 Δ = ( 8 − 14 i)² − 4*( − 1 + 3 i)*( − 11 + 23 i) = = 64 − 224 i + 196 i² − 4*( 11 − 23 i − 33 i + 69 i²) = = 64 − 224 i − 196 − 4*( 11 − 56 i − 69) = = − 132 − 224 i − 4*( − 58 − 56 i) = − 132 − 224 i + 232 + 224 i = 100 √Δ = 10 więc

	− 8 + 14 i − 10		− 18 + 14 i
z1 =		=		=
	2*( − 1 + 3 i)		2*( − 1 + 3 i )

	− 9 + 7 i		− 9 + 7i		− 1 − 3 i
=		=		*		=
	− 1 + 3 i		− 1 + 3i		− 1 − 3 i

	9 + 27 i − 7 i − 21 i2		30 + 20 i
=		=		= 3 + 2 i
	1 − 9 i2		10

	− 8 + 14 i + 10		2 + 14 i
z2 =		=		=
	2*( − 1 + 3 i)		2*( − 1 + 3 i)

	1 + 7 i		1 + 7 i		− 1 − 3 i
=		=		*		=
	− 1 + 3 i		− 1 + 3 i		− 1 − 3 i

	− 1 − 3 i − 7 i − 21 i2		20 − 10 i
=		=		= 2 − i
	1 − 9 i2		10

Janek191: z.1 b i² = − 1 ( 1 + i) z² − ( 4 + 6 i) z + 7 + 9 i = 0 Δ = [ −( 4 + 6 i)]² − 4*( 1 + i)*( 7 + 9 i ) = 16 + 48 i + 36 i² − 4*(7 + 9 i + 7 i + 9 i²) = = 16 + 48 i − 36 − 4*(16 i + 7 − 9 ) = − 20 + 48 i − 4*( − 2 + 16 i ) = = − 20 + 48 i + 8 − 64 i = − 12 − 16 i = 4*( − 3 − 4 i) = 2²*( 1 − 2i)² więc √Δ = 2*(1 − 2i) = 2 − 4 i zatem

	4 + 6 i − 2 + 4 i		2 + 10 i		1 + 5 i
z1 =		=		=		=
	2*( 1 + i)		2*( 1 + i)		1 + i

	( 1 + 5 i)*( 1 − i)		1 − i + 5 i − 5 i2
=		=		=
	(1 + i)*( 1 − i)		1 − i2

	6 + 4 i
=		= 3 + 2 i
	2

	4 + 6 i + 2 − 4 i		6 + 2 i		3 + i
z2 =		=		=		=
	2*( 1 + i)		2*( 1 + i)		1 + i

	( 3 + i)*( 1 − i)		3 − 3 i + i − i2
=		=		=
	( 1 + i)*( 1 − i)		1 − i2

	4 − 2 i
=		= 2 − i
	2

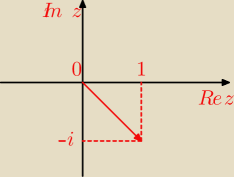
Janek191: z.2 a) z₁ = 1 − i I z₁ I = √1² + (−1)² = √2

	1		√2
cos α =		=
	√2		2

	− 1		√2
sin α =		=
	√2		2

więc

	π
α = − 45o = −
	4

czyli

	π		π
z1 = I z1 I*( cos α + i sin α) = √2*( cos(−		) + i sin ( −		)) =
	4		4

	π		π
= √2*( cos		− i sin		)
	4		4

	π		π
( z1)14 = (√2)14*( cos (		*14) − i sin (		*14)} =
	4		4

	7		7		π		π
= 27*( cos		π − i sin		π} = 128*(cos (π+		) − i sin(π +		)) =
	2		2		2		2

	π		π
= 128* ( − cos		− i *( − sin		)) = 128*( 0 + i) = 128 i
	2		2

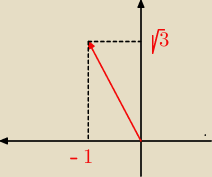
Janek191: cd. z.2 a) z₂ = − 1 + √3 i I z₂ I = √ (−1)² + (√3)² = 2

	− 1
cos α =
	2

	√3
sin α =
	2

więc

	2π
α = 120o =
	3

zatem

	2π		2π
z2 = 2*( cos		+ i sin		)
	3		3

oraz

	2π		2π
( z2)14 = 214*( cos(		*14) + i sin (		*14)) =
	3		3

	28π		28π		4π		4π
= 214*( cos		= i sin		) = 214*(cos		= i sin		) =
	3		3		3		3

	π		π		1		√3
= 214* ( − cos		+ i*( − sin		) = 214*( −		− i		)
	3		3		2		2

J:

	7		π
@Janek ...		π = 4π −		...
	2		2

Janek191: z.2 a) cd.

z114		27 i
	=		=
z214		214*( − 0,5 − 0,5√3 i )

	27 i		i
=		=		=
	213*( − 1 − √3 i)		26*( − 1 − √3 i)

	i*( − 1 + √3 i)
=		=
	26*( −1 − √3 i)*( −1 + √3 i)

	− √3 − i		− √3 − i		1
=		=		=		*( − √3 − i)
	26*( 1 − 3 i2)		26*4		28

Janek191:

7		4 π + 3 π		π
	π =		= 2π + π +
2		2		2

Janek191: z. 2 b) ( − 1 − i )¹⁷*( √3 − i)²¹ = Robimy analogicznie jak a)

Janek191: z.3 A − macierz kwadratowa stopnia n Def. Macierz B nazywamy macierzą odwrotną do macierzy A ⇔ A*B = I i B*A = I gdzie I − macierz jednostkowa stopnia n. B oznaczamy przez A⁻¹. ========================= Poczytaj sobie : W. Krysicki " Analiza matematyczna w zadaniach" część I. s. 146 − 184 Jest w pdf.

Janek191: O liczbach zespolonych poczytaj np. W. Krysicki jw. s. 135 − 140