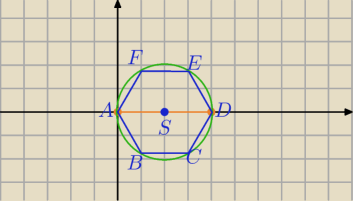
 ok , więc AD = 4 , czyli punkt S= ( 2,0 ),podzieliłem sześciokąt na 6 trójkątów równobocznych
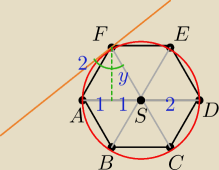
z rysunku łatwo określić,że pierwszą współrzędna punktu F jest 1 −−−> F= ( 1,yf )
drugą obliczę z tw. Pitagorasa : 12 + yf2 = 22 −−−> yf = √3
F= ( 1,√3 )
następnie obliczę równanie prostej SF
S= ( 2,0 ) , F= ( 1,√3 )
(y−0)(1−2) − (√3−0)(x−2) = −y − √3x − 2√3 −−−> y= −√3x + 2√3
zaznaczony kąt jest kątem prostym więc a1*a2= −1
ok , więc AD = 4 , czyli punkt S= ( 2,0 ),podzieliłem sześciokąt na 6 trójkątów równobocznych
z rysunku łatwo określić,że pierwszą współrzędna punktu F jest 1 −−−> F= ( 1,yf )
drugą obliczę z tw. Pitagorasa : 12 + yf2 = 22 −−−> yf = √3
F= ( 1,√3 )
następnie obliczę równanie prostej SF
S= ( 2,0 ) , F= ( 1,√3 )
(y−0)(1−2) − (√3−0)(x−2) = −y − √3x − 2√3 −−−> y= −√3x + 2√3
zaznaczony kąt jest kątem prostym więc a1*a2= −1
| √3 | ||
−√3*a2= −1 −−−> a2= | ||
| 3 |
| √3 | ||
y= | ( x −1 ) + √3 | |
| 3 |
| √3 | √3 | |||
y= | x − | + √3 | ||
| 3 | 3 |
| √3 | √3 | 3√3 | ||||
y= | x − | + | ||||
| 3 | 3 | 3 |
| √3 | 2√3 | |||
y= | x + | |||
| 3 | 3 |

