bardzo proszę o pomoc miki: 1. Wykaż, że jeżeli w trójkącie ostrokątnym o kątach ostrych α i β zachodzą związki

	√15		3√15
sinα=		, sinβ=		to długości boków tego trójkąta tworzą ciąg arytmetyczny.
	8		16

2. Podstawa trapezu wpisanego w okrąg o promieniu r jest średnicą tego okręgu a przekątne trapezu tworzą kąt 60 stopni.Oblicz pole trapezu. 3. Dane są trzy punkty A(6,−2) B(0,4) C(−8,−4) Wyznacz współrzędne takiego punktu D należącego do prostej y=−8 aby na czworokącie ABCD można było opisać okrąg.

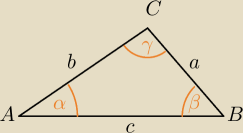Mila: Z tw. sinusów:

a		√15
	=2R⇔a=2R*sinα=2R*		⇔
sinα		8

	R√15
a=
	4

=============

b		3√15
	=2R⇔b=2R*
sinβ		16

	3R√15
b=
	8

===========

c
	=2R⇔c=2R*sin(180−(α+β))=2R*sin(α+β)
sinγ

(*) sin(α+β)=sinα*cosβ+sinβ*cosα

	7
cosα=√1−(15/64)=
	8

	11
cosβ=√1−(9*15/256)=
	16

po podstawieniu do wzoru (*)

	√15
sin(α+β)=
	4

	R√15
c=
	2

============= Teraz sprawdź, że b−a=c−b

miki: dziękuje a mogę też liczyć na pomoc z 2 i 3?

Mila: Po 20, jeśli nikt nie rozwiąże.

miki: Dziekuje bardzo

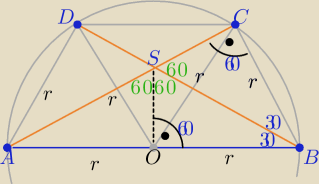Eta: Taki trapez składa się z trzech trójkątów równobocznych o boku długości "r"

	r2√3
zatem P(trapezu)= 3*
	4

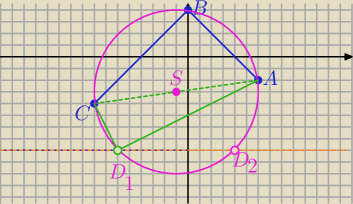Mila: 3) Dane są trzy punkty A(6,−2) B(0,4) C(−8,−4) Wyznacz współrzędne takiego punktu D należącego do prostej y=−8 aby na czworokącie ABCD można było opisać okrąg. Jeżeli czworokąt jest wpisany w okrąg, to suma kątów przeciwległych ma miarę 180^o. Przypuszczam, że AB⊥BC Prosta AB: y=ax+4 −2=6a+4⇔6a=−6 a=−1 AB: y=−x+4 Prosta BC: y=mx+4 −4=−8*m+4⇔−8=−8m⇔m=1 BC: y=x+4 m*a=1*(−1)=−1⇔proste są prostopadłe.⇔∡D=90^o AC jest średnicą okręgu opisanego na ABCD. S=(−1,−3) środek AC, |AS|=√7²+1²=√50 −promień okręgu ∡CD₁A=90^o jako wpisany w okrąg oparty na średnicy (x+1)²+(y+3)²=50, y=−8 (x+1)²+(−8+3)²=50⇔ (x+1)²+25=50 (x+1)²=25 x+1=5 lub x+1=−5 x=4 lub x=−6 D₁=(−6,−8) D₂=(4,−8) =============