Analiza matematyczna Saris: Egzamin Analiza. http://zapodaj.net/5256a1b43fb9b.jpg.html Jak zrobić 2/3? 4. zrobiłem 5. a) zbadac pochodną, f'(x)=0 dla x=0 f(0)=0. Jedyny problem jak pokazać, że e^x2−1≥0 zawsze? Bo wtedy x=0 będzie minimum, więc f(x)=e^x2−1−x²≥0 zawsze.

	1
b)ex2≥1+x2 ⇔ e−x2≤		, a całka z prawej strony to arctgx i na zadanym
	1+x2

przedziale zbiega do π, więc pokazanie, że nasza całka jest ≤ π to koniec? 6. ∫√1+e^x2 Jakiś szybki sposób? Ja robiłem eulerem−>ułamkami prostymi − MASAKRA. x2=x² Prawdopodobnie obleje, bo mi teoria nie podeszła i pierwszy raz w życiu widziałem zadanie typu 2/3. 3 kojarze coś z liceum, ale jak to połączyć z całkami to nie wiem... Jak oceniacie egzamin? Jak na I termin to wydaje mi sie trochę za trudny Za zdanie ćwiczeń powinna być nagroda w postaci łatwiejszego egzaminu Jednak nie...

Godzio: 2. Pokaż, że pochodne są równe (lewej i prawej strony, powinny się oczywiście 0 bo (π)' = 0) i istnieje x₀ dla którego zachodzi równość między funkcjami (x₀ = 1) Twierdzenie o tożsamości 3. Można podać konkretne współrzędne wierzchołków tego prostokąta (będą symetryczne względem OX i OY), policzyć długość odcinków i pole prostokąta to a*b i tam szukamy maksimum

Godzio: 5. f(x) = e^x2 − 1 − x² f'(x) = 2xe^x2 − 2x = 2x(e^x2 − 1) = 0 ⇔ x = 0 e^x2 − 1 ≥ e⁰ − 1 = 1 − 1 = 0 (bo x² ≥ 0) stąd f' zmienia znak z − na + zatem w 0 jest minimum lokalne stąd f(x) ≥ f(0) ⇔ e^x2 − 1 − x² ≥ 0 ⇔ e^x2 ≥ x² + 1

Godzio: b) Ok

Godzio: 6. (e^x)² = e^2x, a nie e^x2 ∫₀¹√1 + e^2xdx e^x = t x = lnt

	1
dx =
	t

0 → 1 1 → e

	√1 + t2
∫1e		dt
	t

A na taką całkę parę metod jest (chociażby Euler, ale też podstawienie trygonometryczne/hiperboliczne)

Saris: No 6 robiłem z eulera i to był duży błąd, bo można było się załamać pod tą całką, ale nie pamiętałem podstawienie tryg. po taką sumę pod pierwiatkiem... Teraz w sumie widzę ze z tgx mogloby coś wyjsc. 2. Nie rozumiem... Ok pochodne sprawdze, ale co potem? Jak się nazywa to tw. nie mogę go znaleźć? 3. Dowolne współrzędne? Maksimum to ekstremum funkcji będzie, ale jak mam to zrobić, mogę policzyć pole tej elipsy ze wzoru, co dalej?

Godzio: Coś nie mogę go znaleźć (może ma jakąś dziwną nazwę, u mnie w książce nazywa się to twierdzenie o tożsamości) Zacytuję: Niech funkcje f i g będą określone na przedziale I zawartym w R oraz niech x₀ ∊ I. Wtedy jeśli 1. f(x₀) = g(x₀) 2. f'(x) = g'(x) dla każdego x ∊ I to f ≡ g na I

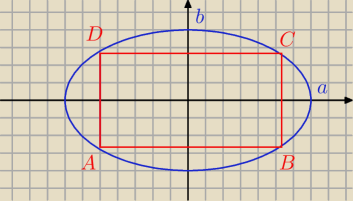
Godzio: Zadanie 3

x2		y2
	+		= 1 ⇒ y = b√1 − x2/a2
a2		b2

A(−x,−b√1 − x²/a²) B(x,b√1 − x²/a²) C(x,b√1 − x²/a²) D(−x,−b√1 − x²/a²) |AB| = ... |BC| = ... P = |AB|*|BC|

kyrtap: W tym 2 jeszcze chyba trzeba podstawić dowolny x czy zgadzają się strony poza liczeniem pochodnych

Kacper:

Saris: Policzyłem tą całkę za pomocą funkcji trygonometrycznych i cyklometrycznych. Sprawdziłby ktoś? http://zapodaj.net/5256a1b43fb9b.jpg.html +C na końcu.

Saris: Woo nie odwróciłem skanu.. Wybaczcie.

Saris: .

Saris: .

Saris: Podane na tacy tylko sprawdzić przejścia

Saris: .

Godzio: Zobacz co nam wysłałeś

Saris: wtf, wczoraj działało. zaraz reupload zrobię.

Saris: http://zapodaj.net/ab6701fb920e3.jpg.html <−− 6 całka trygonometrycznie http://zapodaj.net/fa16930f19710.jpg.html <−− 6 cała Euler itd. http://zapodaj.net/0445e4994a060.jpg.html <−− zad 3. Dobrze i czy czegoś brakuje jeszcze?

Godzio: Na początku błąd w zapisie, na który i tak nie patrzysz, pisałem już o tym: (e^x)² = e^2x, a nie e^x2 (zapisujesz to drugie, liczysz dla pierwszego − czyli dobrze)

Godzio: 1. Całka trygonometrycznie − ok, ale tą moćna łatwiej:

	1		sinx		sinx
∫		dx = ∫		= ∫		dx
	sinx		sin2x		1 − cos2x

cosx = t −sinxdx = dt

dt

dt

1

1

1

1

−∫

= ∫

=

∫(

−

)dt =

ln|U{t −

1 − t2

t2 − 1

2

t − 1

t + 1

2

1}{t+1}|

Godzio: Euler wszystko poprawnie, aczkolwiek konkretnych wyników nie sprawdzam, chodzi o metodę, a nie o wynik

Godzio: Zad 3. |AB| = √4x² = 2|x| = 2x (wypada napisać, że x > 0) W pochodnej zjadłeś "−x²" Jakbyś później sprowadzał do wspólnego mianownika to by się to uprościło, popraw

Saris: Jak to zjadłem. To jest pochodna z illoczynu. to najpierw całka z pierwiastka: 1/2p() i z tego co jest pod piewiastkiem: (−2x/a²). Nie wiem co zjadłem.

Godzio: x z przodu drugiego czynnika i −2x, gdzie znikło?

Saris: P(x) = 4bx * √1−x²/a² P'(x) = (4bx)' * √1−x²/a²+4bx * (√1−x²/a²)' = 4b* √1−x²/a² + 4bx*

	1
		*(−2x/a2)
	2√1−x2/a2

Godzio: Do tego momentu jest ok, dalej zniknęło Ci

	1		−2x
4bx *		* (		)
	2√1 − x2/a2		a2

Saris: ahaaa ja to skróciłem, nie wiem czemu..

Saris: wyjdzie AB=√2a, AD=2b/√2 ?

Godzio: Na to wygląda