matematykaszkolna.pl
przedziay monotonicznosci i ekstremum funkcji evilon: wyznacz przedzialy monotonicznosci i ekstremum funkcji y = 4x1+ x2
3 lut 12:17
Dawid: Wyznacz dziedzinę Policz pierwszą pochodną Przyrównaj pierwszą pochodną do zera
3 lut 12:18
evilon: zaczalem od dziedziny a mianowicie 1 + x2 nierowne 0 x2 nierowne −1 i dalej mam ząg
3 lut 12:24
J: D = R .. teraz pochodna...
3 lut 12:25
evilon: y' = (4x1+x2) y'= −41+x2
3 lut 12:30
Dawid: co tam jest w liczniku za liczba ?
3 lut 12:31
J: ale skąd ...? wzór na pochodną ilorazu ...
3 lut 12:31
Eve:
f f'*g−f*g' 
'=
g g2 
3 lut 12:32
evilon: w liczniku jest −4
3 lut 12:32
Dawid:
 4x (4x)'(1+x2)−4x(1+x2)' 
(
)'=
= dokończ
 1+x2 (1+x2)2 
3 lut 12:33
Dawid: no to zamiast 4x wpisz −4
3 lut 12:33
Eve: evilon zamiast małego u pisz duże U
3 lut 12:35
evilon: y'= 4x /1+x2 = 4 + 4x2 −8x2 / (1+x2)2 = 4 − 4x2 / (1 + x2)2
3 lut 12:36
J: dalej źle...
3 lut 12:38
Dawid: po co przepisujesz na głupiegoemotka Piszesz że co innego jest w licznikuemotka
3 lut 12:38
Dawid:
−4 (−4)'(1+x2)+4(4+1+x2)' 
=
= dokończ
1+x2 (1+x2)2 
3 lut 12:41
evilon:
8x 
? juz nie wiem co zle robie
(1+x2)2 
3 lut 12:46
Eve: −4+20=? −4x2+4x2=?
3 lut 12:50
J: teraz masz dobrze...emotka
3 lut 12:51
Dawid: (−4)'=0 (1+x2)'=2x Dokończ. I tam w liczniku u mnie jest błąd 4(1+x2)' ma byc
3 lut 12:52
J:
 8x 
f'(x) =
 (1+x2)2 
3 lut 12:52
Dawid: Racja jest dobrze. Teraz przyrównaj pochodną do zera
3 lut 12:53
J: i sprawdź, czy zmienia znak i w jaki sposób...
3 lut 12:54
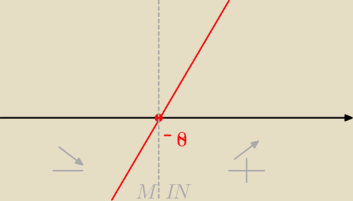
Dawid: rysunekAlbo. Bez tego minusa przed zerem emotka
8x 
=0/*(1+x2)2
(1+x2)2 
8x=0 x=0 F0=..
3 lut 12:59
evilon: z pochodnej wynika ze dziedzina sie zgadza D=R 8x = 0 x = 0
3 lut 13:01
evilon: f(0) = 0
3 lut 13:04
J: gdzie funkcja maleej, a gdzie rośnie...?
3 lut 13:05
Dawid: Masz pokazane wszystko powyżej evilon. Rysujesz wykres pierwszej pochodnej i odczytujesz.
3 lut 13:07