Nierownosc z funkcja kwadratową i wartością bezwględną
Ney: Naszkicuj wykres funkcji i rozwiaz nierownosc x
2−|x−4|≥−2.
Jak ro rozwiazac? nie wychodzi mi

2 lut 22:58
Marcin:
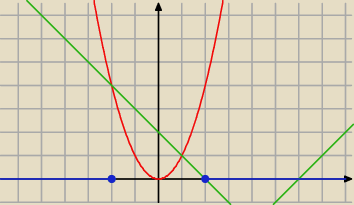
x
2≥−2+|x−4|
x∊...
2 lut 23:05
Marcin: Oczywiście ta prawa niebieska kropka ma być przesunięta o jedną kratkę.
2 lut 23:07
Ney: Moglbys mi to wytlunaczyc jak to wyszlo?
2 lut 23:08
Marcin: Dodałem obustronnie do nierówności |x+4| i później narysowałem dwie osobne funkcje.
2 lut 23:19
Ney: Ja probowalem narysowac dwie funkcje − x2+ Oraz y=|x+4|. odbilem w przypadku drugim to co pod
osia. Ale nie wyszlo mi nic z tego
2 lut 23:24
Ney: x2 + 2 mialo byc, zle napisalem
2 lut 23:26
PW: Niestety, trzeba narysować
g(x) = x2 − x + 4 dla x ≥ 4
oraz
h(x) = x2 + x − 4 dla x < 4
− skleić takie dwa "kawałki parabol".
Kiedy to narysujemy, dodać prostą y = −2, rozwiązanie zadanej nierówności będzie widoczne
"gołym okiem".
2 lut 23:29
Marcin: Oczywiście to nie jest wykres Twojej funkcji. To jest wykres ułatwiający rozwiązanie
nierówności.
2 lut 23:32
Mila:
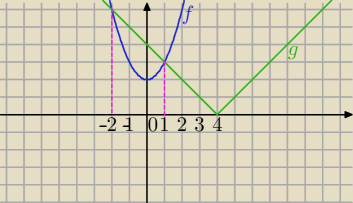
Metoda graficzna: ( nie zawsze dokładna)
x
2−|x−4|≥−2.⇔
x
2+2≥|x−4|
f(x)=x
2+2
g(x)=|x−4|
Rysujemy wykresy obu funkcji w jednym układzie wsp. i odczytujemy dla jakich x wykres f(x) leży
nad wykresem funkcji g(x).
f(x)≥g(x)⇔x≤−2 lub x≥1
Metoda algebraiczna
=================
x
2−|x−4|≥−2
|x−4|=x−4 dla x≥4
Wtedy mamy nierówność:
x
2−x+4+2≥0 i x≥4
x
2−x+6≥0 nierówność spełniona , Δ=1−24<0
(*) x≥4
====
|x−4|=−x+4 dla x<4
Wtedy:
x
2−(−x+4)+2≥0
x
2+x−4+2≥0
x
2+x−2≥0
Δ=1+8=9
(**) x≤−2 lub x≥1 i x<4
=============
(*) lub (**)⇔
x≤−2 lub x≥1
2 lut 23:55
Ney: Mila, dzieki za dokladne rozwiazanie ! Czy moglbyn prosic jakis kontakt do Ciebie? W sprawie
korepetycji.
3 lut 18:46

 x2≥−2+|x−4|
x∊...
x2≥−2+|x−4|
x∊...
 Metoda graficzna: ( nie zawsze dokładna)
x2−|x−4|≥−2.⇔
x2+2≥|x−4|
f(x)=x2+2
g(x)=|x−4|
Rysujemy wykresy obu funkcji w jednym układzie wsp. i odczytujemy dla jakich x wykres f(x) leży
nad wykresem funkcji g(x).
f(x)≥g(x)⇔x≤−2 lub x≥1
Metoda algebraiczna
=================
x2−|x−4|≥−2
|x−4|=x−4 dla x≥4
Wtedy mamy nierówność:
x2−x+4+2≥0 i x≥4
x2−x+6≥0 nierówność spełniona , Δ=1−24<0
(*) x≥4
====
|x−4|=−x+4 dla x<4
Wtedy:
x2−(−x+4)+2≥0
x2+x−4+2≥0
x2+x−2≥0
Δ=1+8=9
Metoda graficzna: ( nie zawsze dokładna)
x2−|x−4|≥−2.⇔
x2+2≥|x−4|
f(x)=x2+2
g(x)=|x−4|
Rysujemy wykresy obu funkcji w jednym układzie wsp. i odczytujemy dla jakich x wykres f(x) leży
nad wykresem funkcji g(x).
f(x)≥g(x)⇔x≤−2 lub x≥1
Metoda algebraiczna
=================
x2−|x−4|≥−2
|x−4|=x−4 dla x≥4
Wtedy mamy nierówność:
x2−x+4+2≥0 i x≥4
x2−x+6≥0 nierówność spełniona , Δ=1−24<0
(*) x≥4
====
|x−4|=−x+4 dla x<4
Wtedy:
x2−(−x+4)+2≥0
x2+x−4+2≥0
x2+x−2≥0
Δ=1+8=9