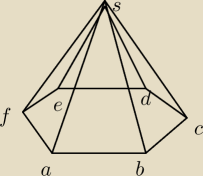
 Dany jest ostrosłup prawidłowy sześciokątny, w którym kąt między krawędziami AS i DS jest równy
α. Wykaż, że cosinus kąta między krawędziami AS i BS jest równy 3+cosα4. Proszę o pomoc,
próbowałam to wyliczyć z tw. cosinusów, ale nie wychodzi.Wyszło mi 3b+cosα4, gdzie b to
krawędź boczna, nie wiem jak pozbyć się tej niewiadomej.
Dany jest ostrosłup prawidłowy sześciokątny, w którym kąt między krawędziami AS i DS jest równy
α. Wykaż, że cosinus kąta między krawędziami AS i BS jest równy 3+cosα4. Proszę o pomoc,
próbowałam to wyliczyć z tw. cosinusów, ale nie wychodzi.Wyszło mi 3b+cosα4, gdzie b to
krawędź boczna, nie wiem jak pozbyć się tej niewiadomej.
| 1 | 1−cosβ | ||
= | |||
| 4 | 1−cosα |
| 3+cosα | ||
cosβ= | ||
| 4 |
