str 170 z 6 Matematyka zakres podstawowy i rozszerzony, własności funkcji

str 170 z 6 Matematyka zakres podstawowy i rozszerzony, własności funkcji Mój nick: Dla jakiej wartości współczynnika a wykres funkcji f(x)=1/2|x|+a wraz z osią OX ogranicza trójkąt o polu równym a)8 b)98. Pomoże ktoś?

2 lut 20:21

Eve: a) a=2 b) a=7

2 lut 20:25

Eve: −2 i −7

2 lut 20:26

J: ..jeśli a >0 , to nie ma trójkąta ... emotka

2 lut 20:27

Mój nick: Nie rozumiem tego zupełnie. Jakim sposobem to zrobiłaś? Moglibyście mi narysować ten wykres funkcji?

2 lut 20:30

Eve: poprawiłam emotka

2 lut 20:30

Eve:

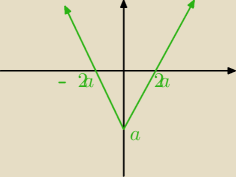
pierwiastki obliczyłam

2 lut 20:32

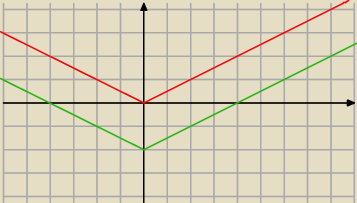
5-latek: rysunek

y=0,5|x| czerwony y=0,5|x| −2 zielony

2 lut 20:35

Mój nick: Dziękuję. Teraz to rozumiem.(:

2 lut 20:47

Eve: no to ok emotka

2 lut 20:48

Dżul: Dlaczego jak a jest większe od 0 to nie ma trojkata?

21 kwi 19:21

wredulus_pospolitus:

	1
1. Zauważ, że funkcja f(x) =		\|x\| + a przyjmuje najmniejszą wartość dla x=0 i jest to
	2

f(0) = a. 2. Jeżeli a>0, to f(x) > 0 dla dowolnego x∊R. 3. Związku z tym, nie ma możliwości aby wykres f(x) PRZECINAŁ oś OX ... co w efekcie daje nam −−−> obszar pomiędzy wykresem funkcji f(x) i osią OX NIE jest trójkątem

21 kwi 19:54