Ostrosłup prawidłowy trójknątny, kąt dwuścienny między ścianami bocznymi.
Greg:
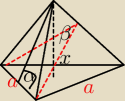
Witam, mam tutaj zadanko, z którym nie mogę się uporać od dłuższej chwili. Treść jest
następująca: W ostrosłupie trójkątnym prawidłowym kąt między ścianą boczą a podstawą jest
równy α. Oblicz ccosinus kąta β między ścianami bocznymi tego ostrosłupa.
Wiem, że zadanie sprowadza się do użycia twierdzenia cosinusów, ale brakuje mi tej długości x,
i
nie mam pojęcia jak do niej dojść. Będę wdzięczny za pomoc
2 lut 19:18
Greg: Help :c
2 lut 19:35
Greg: odświeżam.
2 lut 19:43
Eve: gdzies to zadanie juz tutaj było, ale go nie umiem znaleźć, ja na niego nie miałam pomysłu
2 lut 19:46
Greg:
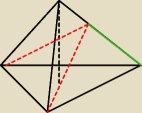
Szukałem, nie znalazłem. Może dało by się znaleźć tą długość zaznaczoną na zielono jakoś. Ktoś
jakiś pomysł sypnie : d ? ?
2 lut 19:54
Eve:
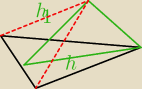
jeszcze mamy taki Δ
2 lut 20:00
Greg: Kurcze, nie mam kompletnie żadnego pomysłu na to. Nie wiem z której strony podejść, za duzo
robi mi się niewiadomych. Pozostaje mi poczekać aż kogoś oświeci . Zadanko jest z zestawów
maturalnych, zostało mi na koniec. Można za nie zgarnąć 7 pkt więc trochę trzeba pokombinować.
2 lut 20:28
Greg: Podbijam.
2 lut 20:53
Eve: zapodałam link, zobaczymy co wymysli Eta albo Bogdan
2 lut 21:15
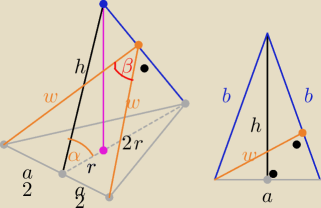
Eta:
| | a | |
W trójkącie ściany bocznej b= √h2+ |
| )2 =......... |
| | 2 | |
i a*h= b*w ⇒ w=....
i z tw. kosinusów
| | 2w2−a2 | |
cosβ= |
| =....... ( uprość "a" |
| | 2w2 | |
dokończ .........
2 lut 22:38
Bogdan:
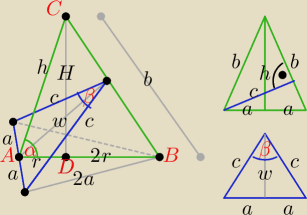
| | a2 | |
Z twierdzenia cosinusów: 4a2 = 2c2 − 2c2cosβ ⇒ cosβ = 1 − 2* |
| |
| | c2 | |
r − długość promienia okręgu wpisanego w podstawę tego ostrosłupa,
| | r | | r2 | |
H = r*tgα, b2 = H2 + 4r2 = r2(tg2α + 4), |
| = cosα ⇒ h2 = |
| |
| | h | | cos2α | |
| | bc | | a | | b | | a2 | | b2 | |
Pole ściany bocznej: a*h = |
| ⇒ |
| = |
| ⇒ |
| = |
| |
| | 2 | | c | | 2h | | c2 | | 4h2 | |
| | b2 | |
cosβ = 1 − 2* |
| = ... |
| | 4h2 | |
2 lut 22:38
Bogdan:

2 lut 22:39
Greg: Dzięki wam za pomoc

.
2 lut 22:50
Eta:
Właśnie miałam pisać,że można też z tgα

2 lut 22:50
Eta:
Dla
Eve 

3 lut 12:24
Eve: a za co?

3 lut 12:34
Eta:
Za linka

Myślałam,że ja dostanę


3 lut 13:39
3 lut 13:46
Dżepetto 18: Myślę i myślę jak odnieść to do mojego zadania:
Czworościan ABCS o krawędzi długości a przecięto płaszczyzną przechodzącą przez punkty A, B i
środek krawędzi CS. Oblicz pole otrzymanego przekroju i cosinus miary kąta nachylenia tego
przekroju do podstawy czworościanu.
Na rysunku u Bogdana mój szukany kąt tworzy szara prosta w oraz wysokość trójkąta w
podstawie 2r+r.
Ktoś coś? U mnie 3 dzień siedzenia nad tym zadaniem.
10 lut 20:05
Dżepetto 18: Może Eta lub Bogdan to zobaczą

10 lut 20:29
Dżepetto 18: Może jednak

10 lut 20:56
Dżepetto 18: :c
10 lut 21:29
Bogdan:

a = 2c − długość krawędzi czworościanu foremnego
| | c√2 | |
Pole przekroju PABD = c*c√2 = c2√2 oraz cosα = |
| = ... |
| | c√3 | |
Rysunek wyjaśnia wszystkie długości
10 lut 21:31
Dżepetto 18: Dziękuję
Bogdan! Już biorę się za analizę

10 lut 21:56
Dżepetto 18: Wszystko przetrawione. Jeszcze x wielkie dzięki; super prosto wytłumaczone

!
10 lut 22:09
Bogdan:

10 lut 22:22
 Witam, mam tutaj zadanko, z którym nie mogę się uporać od dłuższej chwili. Treść jest
następująca: W ostrosłupie trójkątnym prawidłowym kąt między ścianą boczą a podstawą jest
równy α. Oblicz ccosinus kąta β między ścianami bocznymi tego ostrosłupa.
Wiem, że zadanie sprowadza się do użycia twierdzenia cosinusów, ale brakuje mi tej długości x,
i
nie mam pojęcia jak do niej dojść. Będę wdzięczny za pomoc
Witam, mam tutaj zadanko, z którym nie mogę się uporać od dłuższej chwili. Treść jest
następująca: W ostrosłupie trójkątnym prawidłowym kąt między ścianą boczą a podstawą jest
równy α. Oblicz ccosinus kąta β między ścianami bocznymi tego ostrosłupa.
Wiem, że zadanie sprowadza się do użycia twierdzenia cosinusów, ale brakuje mi tej długości x,
i
nie mam pojęcia jak do niej dojść. Będę wdzięczny za pomoc
 Szukałem, nie znalazłem. Może dało by się znaleźć tą długość zaznaczoną na zielono jakoś. Ktoś
jakiś pomysł sypnie : d ? ?
Szukałem, nie znalazłem. Może dało by się znaleźć tą długość zaznaczoną na zielono jakoś. Ktoś
jakiś pomysł sypnie : d ? ?
 jeszcze mamy taki Δ
jeszcze mamy taki Δ



 .
.




 Myślałam,że ja dostanę
Myślałam,że ja dostanę 


 łap
łap 


 a = 2c − długość krawędzi czworościanu foremnego
a = 2c − długość krawędzi czworościanu foremnego

 !
!
