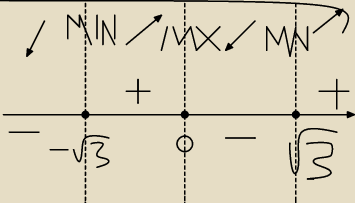przedział monotoniczności
paw:
2 lut 13:56
J:
1) Dziedzina.
2) Pochodna = ...?
2 lut 13:57
paw: dziedzina x∊(−∞,−1)u(1,∞)
pochodna wychodzi straszna
2 lut 13:58
paw: w pochodnej wychodzi x2(−x2−3)
|
0
2 lut 13:59
paw: w sensi licznik
ze wzoru"
2 lut 14:00
J:
dziedzina źle...
2 lut 14:02
paw: x2−1>0
x2>1
x>1 lub x<−1
2 lut 14:07
J:
a mianownik nie może być ujemny...?
2 lut 14:08
paw: x≠1 lub x≠−1***
2 lut 14:13
J:
teraz dobrze..
| | x2(x2−3) | |
f'(x) = |
| .. teraz analizuj pochodną .. |
| | (x2−1)2 | |
2 lut 14:14
J:
co do dziedziny: x ≠ 1 i x ≠ − 1
2 lut 14:15
paw: czemu w liczniku x4 jest dodatnia ?
odejmowaliśmy 3x4−4x4
2 lut 14:17
J:
a skąd masz − 4x4..?
2 lut 14:20
paw: aaa nie przepraszam, mój głupi błąd,niedopatrzenie...
ten minus mi wadził
wiec dalej x2(x2−3)
| |
0 √3 u −√3
2 lut 14:24
J:
gdzie pochodna ( i jak ) zmienia znak...?
2 lut 14:26
paw: no chyba tak jak we wzorach...
2 lut 14:59
J:
konkretnie ...
2 lut 15:00
2 lut 15:05
J:
aby określić monotoniczność funkcji, musisz określić jak zmienia sie znak pochodnej w punktach,
w których sie ona zeruje...
2 lut 15:07
paw:
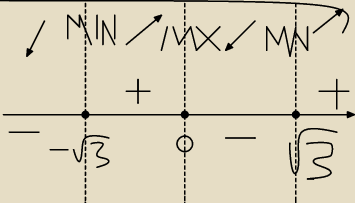
2 lut 15:13
paw: ooo, w sensie od góry przechodzi przed √3 i później przez 0 i −√3
2 lut 15:14
J:
w punkcie: x = 0 jest odbicie .... nie ma zmiany znaku ...
2 lut 15:20