trzeba tylko umiejętnie rozwiązać to równanie na końcu
Kuba:
Witam, miałem egzamin wyliczyłem i zaznaczyłem odpowiedź C) 0,8788 ale nie jestem pewien, bo
nie pamiętam jak do tego doszedłem... Czy jest mi ktoś w stanie pomóc, gdyż wyniki mam za parę
dni i nie wiem czy przygotowywać się do poprawy. Jeżeli to zadanie mam dobrze to zdałem !
W celu oszacowania wartości oczekiwanej w populacji pobrano próbę 400 elementową i otrzymano
przedział ufności (15,8; 16,575). Wiadomo, że wariancja wynosi 25. Jaki był poziom ufności?
A) 0,9836 B) 0,9282 C) 0,8788 D) 0,9642 E) żadna z powyższych
n=400
wariancja(s2) = 25, więc odchylenie standardowe(δ)= 5
z podanego przedziału wyliczam jego długość d= 0,775
a co za tym idzie mogę podstawić do wzoru
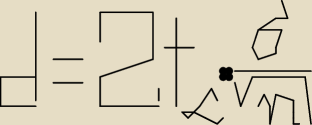
d=2*tα*(sigma/pierwiastek z n)
a więc 0,775 = 2tα 0,25 (trzeba tylko rozwiązać to równanie)
 Witam, miałem egzamin wyliczyłem i zaznaczyłem odpowiedź C) 0,8788 ale nie jestem pewien, bo
nie pamiętam jak do tego doszedłem... Czy jest mi ktoś w stanie pomóc, gdyż wyniki mam za parę
dni i nie wiem czy przygotowywać się do poprawy. Jeżeli to zadanie mam dobrze to zdałem !
W celu oszacowania wartości oczekiwanej w populacji pobrano próbę 400 elementową i otrzymano
przedział ufności (15,8; 16,575). Wiadomo, że wariancja wynosi 25. Jaki był poziom ufności?
A) 0,9836 B) 0,9282 C) 0,8788 D) 0,9642 E) żadna z powyższych
n=400
wariancja(s2) = 25, więc odchylenie standardowe(δ)= 5
z podanego przedziału wyliczam jego długość d= 0,775
a co za tym idzie mogę podstawić do wzoru
d=2*tα*(sigma/pierwiastek z n)
a więc 0,775 = 2tα 0,25 (trzeba tylko rozwiązać to równanie)
Witam, miałem egzamin wyliczyłem i zaznaczyłem odpowiedź C) 0,8788 ale nie jestem pewien, bo
nie pamiętam jak do tego doszedłem... Czy jest mi ktoś w stanie pomóc, gdyż wyniki mam za parę
dni i nie wiem czy przygotowywać się do poprawy. Jeżeli to zadanie mam dobrze to zdałem !
W celu oszacowania wartości oczekiwanej w populacji pobrano próbę 400 elementową i otrzymano
przedział ufności (15,8; 16,575). Wiadomo, że wariancja wynosi 25. Jaki był poziom ufności?
A) 0,9836 B) 0,9282 C) 0,8788 D) 0,9642 E) żadna z powyższych
n=400
wariancja(s2) = 25, więc odchylenie standardowe(δ)= 5
z podanego przedziału wyliczam jego długość d= 0,775
a co za tym idzie mogę podstawić do wzoru
d=2*tα*(sigma/pierwiastek z n)
a więc 0,775 = 2tα 0,25 (trzeba tylko rozwiązać to równanie)