określ dla jakich przedziałów funkcja jest rosnąca/ malejąca xyz: a) f(x)= (1−x)/(2+x) b) f(x)=3sin(2x) c)f(x)=x²(4−x) d)f(x)=4e²*x −3 e)f(x)= 2x³ −4x²−5x+9

Janek191:

	1 − x
a) f(x) =		; x ≠ − 2
	2 + x

	− 1*( 2 + x) − (1 − x)*1		− 2 − x − 1 + x
f '(x) =		=		=
	( 2 + x)2		( 2 + x)2

	−3
=		< 0 dla x ∊ Df
	(2+x)2

Funkcja maleje w przedziałach : ( − ∞ ; − 2), ( − 2; + ∞ ).

xyz: Dzięki a pozostałe wiesz jak zrobić

Janek191: Robimy tak samo jak a)

xyz: c)sprawdzi to ktoś? f'(x)=4x²−x³=−3x²+8x f'(x)=x(−3x+8) x=0 x=(2²₃) F.malejąca: (−∞,0),((2²₃,+∞)

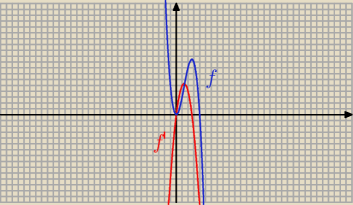Janek191: Źle : f(x) = 4 x² − x³ więc

	8
f' (x) = 8 x − 3 x2 = x*( 8 − 3 x) = 0 ⇔ x = 0 lub x =
	3

	2
f' ( x) > 0 dla x ∊ ( 0 ; 2		)
	3

	2
więc funkcja f rośnie w ( 0; 2		)
	3

	2
a maleje w : ( − ∞ ; 0) , ( 2		; + ∞ )
	3

xyz: dzięki