Równania kwadratowe z wartością bezwzględną i parametrem Paweł: Zbadaj liczbę rozwiązań równania w zależności od parametru k a) |x²−4|=k²+3 b) −x²+2|x|=k²−2 c) |¹₂x²−2x+1|=2k−k² d) 6x²−12|x|=k²+3k−4

Paweł: up proszę o rozwiązanie w szczególności podpunktu c)

Paweł: up

Paweł: up

1: jest wartość bezwzględna więc w c: prawa str równania powinna być większa/równa 0 i mamy k(2−k) większe równe 0

Paweł: tak, ale mam podać dla jakich wartości k równanie ma 0,2,3 lub 4 rozwiązania

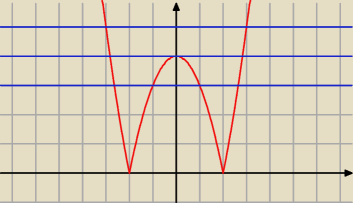
ICSP: Wszystko zależy od tego jak narysujesz wykres. Z niego widać, od razu. że jeżeli : Równanie posiada dwa pierwiastki jeśli k² + 3 > 4 Równanie posiada trzy pierwiastki jeśli k² + 3 = 4 Równanie posiada cztery pierwiastki jeśli k² + 3 ≥ 3 ∧ k² + 3 < 4 Ponieważ zbiorem wartości k² + 3 względem k jest przedział [3 , + ∞) wartości które są mniejsze od 3 nie rozpatruje. Wszystkie inne przykłady robisz analogicznie. Jedyny problem w narysowaniu wykresu.

Paweł: a skąd się wzięło "zbiorem wartości k2 + 3 względem k jest przedział [3 , + ∞)" ? Proszę o wyjaśnienie

Paweł: up

Paweł: up

Paweł: up

ICSP: Nie wiesz jak się wyznacza zbiór wartości funkcji kwadratowej ?

Paweł: wiem wszystko jasne, dziękuję bardzo za pomoc