powtórka
Kinia: Z punktu A=(4,1) poprowadzono proste styczne do okręgu x2+y2+4y+3=0 . Oblicz pole trojkąta
ABC, gdzie wierzchołki B i C są punktami styczności.
31 sty 20:25
Frost: Masz odpowiedzi ?

31 sty 20:27
31 sty 20:28
Frost: Ok, robie, jak zrobię dam znać

31 sty 20:31
Kinia: ok, dziękuję


31 sty 20:38
Frost: Zawsze robię to zadanie na taki sposób
1) zwijam wzór na okrąg
2) prosta y=ax+b jest styczna do okręgu i do tej prostej należy punkt A.
3) podstawiam do prostej i wyliczam b=1−4a
4) wzór prostej y=ax+1−4a
5) prosta jest styczna więc robie układ równań i wstawiam równanie prostej za y w okręgu
6)doprowadzam równanie do postaci równania kwadratowego
7)Δ=0 bo chcemy 1 punkt wspólny.
8) wychodzą nam dwa współczynniki a
1 i a
2
9) mamy równania prostych. Podstawiamy jeszcze raz do równania okręgu i liczymy punkty
styczności B i C
10) obliczamy współrzędne wektorów AB i AC
| | 1 | |
11) pole trójkąta to |
| det(AB, AC) |
| | 2 | |
Czasochłonne ale sprawdzone. Spróbuje wymyślić łatwiejszą metodę.
31 sty 20:39
Kinia: wiem, znam tą metodę, ale jakby o nią tu chodziło to bym nie poprosiła o pomoc

wychodzą
"brzydkie" liczby gdy będziemy tak rozwiązywać

trzeba jakoś inaczej ...
31 sty 20:41
Frost: doszedłem do liczenia współczynników i wyszły mi
31 sty 20:42
Kinia: no to mi nie powiesz, że ładne?


31 sty 20:42
Frost: no nie ale cóż.. Jak chcesz inaczej obliczyć punkty wspólne prostych z okręgiem jak nie
będziesz miała równań prostych ?

31 sty 20:43
Kinia: wskazówka w tym zbiorze brzmi: oblicz |AS|, |AB| i szukaj trójkątów podobnych, tylko nie bardzo
mogę je dostrzec
31 sty 20:45
Frost: Dobra , AS możemy obliczyć ale AB? nie mając współrzędnych punktu B? wydaje mi się, że ta
wskazówka jest do tego by obliczyć już pole

31 sty 20:46
Kinia: |AB| też chyba możemy, bo mamy promień i |AS| i tam będzie trójkąt prostokątny... ? czy źle
myślę?
31 sty 20:48
Frost:
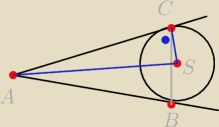
Dobrze mówisz
31 sty 20:50
Kinia: ale czy to nam coś daje ?

31 sty 20:53
Frost: Próbuję coś wymyślić ale nic mi nie przychodzi do głowy
Trójkąt podobny do ASC to ASB

31 sty 20:55
Kinia: chyba widzę trójkąty podobne, trzeba skorzystać z kąta dopisanego
31 sty 20:57
Frost: O widzisz, zrób i daj znać jak wyjdzie

31 sty 20:58
Kinia: niech K będzie punktem przecięcia AS i BC, wtedy ΔABS ~ ΔSKB
31 sty 20:58
Frost: Okey, licz dalej

31 sty 21:00
Kinia: ok

31 sty 21:00
===:
policz tylko |AO| ...dalej "zwykłą geometrią" −

31 sty 21:04
Frost: To będzie |AS|

31 sty 21:04
===:
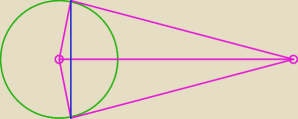
... i zauważ podobieństwo trójkątów
31 sty 21:07
Kinia: Udało się

31 sty 21:09
Kinia: Zrobione
31 sty 21:09
===:
może być |AS| ... ja jako środek okręgu przyjmuję O=(0, −2)
31 sty 21:09
Frost: Jak kto woli

ja pisałem adekwatnie do mojego rysunku

31 sty 21:10
Frost:
Kinia

31 sty 21:13
Kinia: Dzięki Frost


31 sty 22:53




 wychodzą
"brzydkie" liczby gdy będziemy tak rozwiązywać
wychodzą
"brzydkie" liczby gdy będziemy tak rozwiązywać trzeba jakoś inaczej ...
trzeba jakoś inaczej ...




 Dobrze mówisz
Dobrze mówisz







 ... i zauważ podobieństwo trójkątów
... i zauważ podobieństwo trójkątów

 ja pisałem adekwatnie do mojego rysunku
ja pisałem adekwatnie do mojego rysunku 



