wsółrzędne Rita: Punkt P należy do odcinka o końcach A(−20;20) i B(60;60). Jeśli 4|BP=|AB|, to jakie współrzędne ma punkt P? Obliczyłam już długość odcinka |AB|=(80;40). Co dalej?|

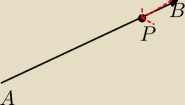
Frost: to nie długość tylko współrzędne wszystko pomyliłaś AB=[80,40] BP=[x−60,y−60] 4(x−60)=80 4(y−60)=40

pigor: ..., z warunków zadania : niech P=(x,y)=? 4|BP|= |AB| ⇒ 4[x−60,y−60]= [80,40] ⇔ [x−60,y−60]= [20,10] ⇔ ⇔ x−60= 20 i y−60= 10 ⇔ (x,y)= 80,70). ...

maturzystka:'(:

maturzystka112: zle pigor ... ma wyjsc inna wróc na lekcje

pigor: ..., no i fajnie, trudno, ale nie chce mi się szukać ewentualnego błędu a lekcje − delikatnie mówiąc − olewam, bo nie muszę już nigdzie wracać

twojstaty: ≥Ωγβ∞

Eta: 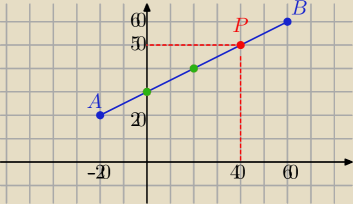P(40,50)

5: ∞ΩΔΔ

Vaadin : Prawidłowa odpowiedź według klucza to P (35,45).

wyjasnienie: Prawidłowa odpowiedź według klucza to P (40,50) , pozdrawiam jeżeli ktoś wracałby do tego zadania

nihygyytu: βγδΔΩα≤⊂∫∞πΩ←→⇒∞Δ∞Δ

nihygyytu:

Matuura : Wystarczy obliczyć współrzędne srodka odcinka: S(AB) =( −20+60/2;20+60/2), czyli S=(20;40) I ponownie srodek odcinka SB, czyli P: P=(20+60/2;40+60/2), czyli P=(40,50) (Bo 4BP=AB. Pierwszy srodek dzieli prostą tak, że 2AS/BS=AB, więc "srodek srodka" podzieli tak, że 4BP=AB)

Matma z wyboru: Kochani 4(60−x,60−y)=(60−−20,60−20) 4(60−x,60−y)=(60+20,60−20) 4(60−x,60−y)=(80,40)/:4 (60−x,60−y)=(20,10) 60−x=20 x=40 60−y=10 y=50

Dupa: O kurwa

Marek pogromca: Xd

chichi:

	−20+3*60		20+3*60
P=(		,		)=(40, 50)
	1+3		1+3