Ostrosłup
lol: W ostrosłupie prawidłowym czworokątnym odległość środka symetrii podstawy od ściany bocznej
jest równa 6. Miara kąta między krawędziami bocznymi ostrosłupa należącymi do jednej ściany
bocznej jest równa 2α. Oblicz objętość tego ostrosłupa.
I mam też pytanie, czy miara kąta między przeciwległymi ścianami bocznymi też jest równa 2α?
Proszę o pomoc
31 sty 16:08
lol: może jednak ktoś ma pomysł? nie musi być pełne rozwiązanie, tylko jakie zależności wykorzystac,
co od czego wyprowadzic mniej wiecej
31 sty 21:20
===:
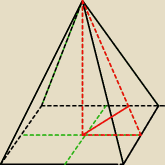
zauważ trójkąty podobne i licz
31 sty 21:35
Mila:
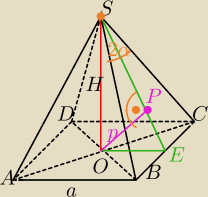
p= |OP|=6
WΔBES:
0.5a=h*tgα
Porównaj pole ΔSOE:
Dalej próbuj sam.
Napisz wynik.
31 sty 21:44
dero2005:
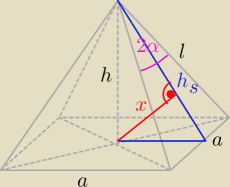
x = 6
h
2 + (
a2)
2 = h
s2 a =
V =
31 sty 21:44
lol: przyjmę oznaczenia z rysunku Mili:
| | 6 | |
H= |
| (z równości pól albo podobieństwa jak dero2005) |
| | tgα | |
z Pitagorasa:
H
2 + (
a2)
2 = h
2
| 36 | | a2 | | a2 | |
| + |
| = |
| (rozszerzam do wspólnego mianownika 4tg2α i daje |
| tg2α | | 4 | | 4tg2α | |
wszystko na lewą stronę, czyli przyrównuje do zero a to znaczy, że licznik musi być równy 0 i
mam cos takiego: )
144 + a
2tg
2α − a
2 = 0
| | 144 | |
a2 = |
| i jeśli wstawie teraz do wzoru na V to ciągle mam niewiadomą tgα, chyba |
| | 1 − tg2α | |
że czegoś nie zauważyłem...
31 sty 22:20
Mila:
α − masz dane, podaj warunki wykonalności (1−tg2α>0 )
Nie masz odpowiedzi do zadania,aby sprawdzić wynik, bo nie przeliczałam do końca.
31 sty 22:35
lol: no α >45 stopni
| | 144 | | 6 | | 288 | |
V mi wychodzi jak coś V = 13 * |
| * |
| = |
| |
| | 1 − tg2α | | tgα | | tgα(1 − tg2α) | |
dzięki za pomoc

31 sty 22:42
Mila:
Wszystko jest dobrze.
31 sty 22:46
Mila:
α<45o
31 sty 22:47
lol: no tak tak, źle spojrzałem na znaki..
31 sty 22:54
 zauważ trójkąty podobne i licz
zauważ trójkąty podobne i licz
 p= |OP|=6
p= |OP|=6
 x = 6
x = 6
