Zadania Blue: Czy te zadania są dobrze zrobione http://i60.tinypic.com/30vj9xf.jpg http://i60.tinypic.com/1znqt0y.jpg http://i58.tinypic.com/wasvft.jpg

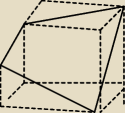
Maslanek: 1. Nie − przekrój nie jest trójkątem To będzie figura takiego rodzaju:

Maslanek: 2. Chyba trochę prościej: x=c*cos15 y=c*sin15

	1		1		1
Stąd √xy=√c2sin15cos15=c*√		sin30 = c*√		=		c
	2		4		2

Maslanek: 3. Ciąg ma być rosnący. Przypuśćmy, że jest geometryczny. Wtedy 9=3²=2*5=10 − sprzeczność.

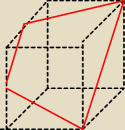
Maslanek: Twój przekrój. Miłe odmóżdżenie

Maslanek: Twój wynik jednak jest całkiem przydatny, bo teraz wystarczy Ci obliczyć tylko pole tego drugiego trójkąta, co nie jest już kłopotliwe

Kacper: Zadanie za 3 pkt No liczymy jakby było za 3 punkty.

	4√2
Przekrojem jest trapez równoramienny o podstawach długości a=4√2 i b=		oraz
	2

ramieniu c=2√5. Liczymy wysokość trapezu: h²+(√2)²=(2√5)² h=√18=3√2

	a+b
P=		*h=3√2*3√2=18
	2

Blue: To ten ciąg mam źle czy dobrze?

Maslanek: Jest w porządku. Pokazuję tylko, że można inaczej Zacznij sobie trochę ufać

Kacper: Myślicie, że to zadanie z ciągiem byłoby tak proste za 4 pkt? A gdzie jest info, że te liczby to kolejne wyrazy ciągu?

dawid wolinski: co to za ksiązka ? prosze o tytuł

Blue: Kaper, ale jak rosnący ma być, no to chyba logiczne....

Blue: Dawid Arkusze z nowej ery

Kacper: Masz odpowiedzi do tego?

Eta:

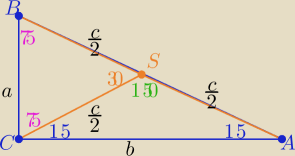
	a*b
P(ABC)=		i P(ABC)= P(ACS) +P(CBS)
	2

	1		c		c		1		c		c		c2
P(ACS)=		*		*		*sin150o =		*		*		*sin30o=
	2		2		2		2		2		2		16

to:

	ab		2c2		c2		c
		=		⇒ ab=		⇒ √ab=
	2		16		4		2

c.n.u

Eta: Można też napisać,że: CS jest środkową trójkąta ABC , to pola trójkątów ACS i BCS są równe , itd...... Blue staraj się podawać jak najprostsze ( mało czasochłonne) rozwiązania a nie "dookoła świata"

bezendu: I może tak na końcu wypada napisać słowo dziękuję, bo pomoc dostajesz za darmola..

Mila: Zadanie z ciągami. Wykazałaś, że 2,3,5 nie mogą być kolejnymi wyrazami c. g., ale może się zdarzyć, że to będą przykladowo: a₁, a₇, a₁₁ Możesz przyjąć, że a₁=2, a_k=3, k>2 a_m=5, m>k Korzystaj własności c. g.

Blue: a więc o to chodzi, rzeczywiście nie napisali, że to są kolejne, dzięki

Blue: Kacper, tak i właśnie były w nich inne odpowiedzi więc chciałam się dowiedzieć czy moje rozwiązania są złe i dlaczego

Kacper: To może podaj ich wersję rozwiązania?

Mila: Nie doczekamy się. Też jestem ciekawa.

kyrtap: Mila korzystając z okazji, Pozdrawiam

Mila: Wzajemnie. Jak tam kolokwium?

kyrtap: o jaki pytasz Milu, chodzi o algebrę?

Mila: Tak.

kyrtap: 5 mam dzięki wam oczywiście dziękuje bardzo

Metis:

Supreme: Blue z jakiego ćwiczenia korzystasz? ps. ile już zrobiłaś?

Mila:

kyrtap: nie słodźcie mi tak bo sami byście równie dobrze a nawet lepiej poradzili sobie

Blue: Przepraszam, że się nie odzywałam, teraz jest już późno, ale jutro Wam mogę wrzucić skany jeśli chcecie

Blue: http://i61.tinypic.com/wrnkph.jpg http://i62.tinypic.com/2mota1t.jpg Proszę

Mila: Tak właśnie to sobie wyobrażałam. Rozwiązanie z trójkątem masz od Maslanka, podobnie od Ety, a z ciągiem masz dobrą podpowiedź 17:30, nawet podobne oznaczenia.

Mila: Zadanie dla Blue Przez jedną krawędź czworościanu foremnego oraz punkt wewnętrzny krawędzi skośnej do niej poprowadzono płaszczyznę.Kąt nachylenia tej skośnej do płaszczyzny przecinającej czworościan ma miarę α. Wiedząc, że krawędź czworościanu ma długość a, oblicz pole otrzymanego przekroju.

Kacper: Ładne zadanko

Blue:

	a2√2
Mila , wyszło mi P =		, dobrze
	4sinα

Mila: Blue, dobrze.

Blue: Wow

Blue: Nie spodziewałam się