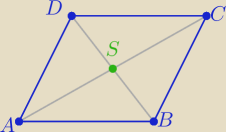
geo analityczna geometrykz: W rombie ABCD przekątne przecinają się w punkcie S(2, −1). Dwa kolejne wierzchołki rombu mają współrzędne A(m, −3) oraz B(m+6, m−5), gdzie m∊R. wyznacz: a)współrzędne wierzchołków rombu b)... c)... d)... myślę, że jak zrobię a), to z resztą sobie poradzę; myślałem nad tym, żeby wyznaczyć proste przechodzące przez AS oraz przez BS(prostopadła do AS), ale nic nie mogę z tym zrobić; ktoś ma jakiś pomysł?

Eta: x_D= 2x_S−x_B i y_D= 2y_S−y_B x_C= 2x_S−x_A i y_C=2y_S−y_A teraz tylko podstaw dane .........

geometrykz: podstawiam i wychodzi: C(4−m,1) oraz D(−m−2, −m+3) i co dalej? po zrobieniu to w ten sposób, jak opisałem wcześniej, zaczynają wychodzić pierwiastki więc albo się machnąłem gdzieś w obliczeniach, albo trzeba to zrobić jakoś inaczej; dodam, że w odpowiedziach: m=0.

Eta: C(4−m,1) , D(−m−2, −m+3) i tak ma być Może jeszcze masz coś podane w treści zadania ?

geometrykz: niestety nie, przepisałem całą treść słowo w słowo.

Eta: Z jakiego zbioru jest to zadanie?

geometrykz: Matematyka zbiór zadań do liceów i techników klasa 3. Zakres rozszerzony; dział geometria analityczna, zadania powtórzeniowe do rozdziału 3. strona 106 zad. 3.200.

Bogdan: |AS|² + |BS|² = |AB|² ⇒ m = 0

Eta: Jasne m=0

Eta: O tej porze już mózg potrzebuje odpoczynku Dobrej nocy

geometrykz: teraz wyszło. dziękuję x)

geometrykz: dobrej nocy, przede mną jeszcze ze dwie godzinki

Eta: Dokończyłeś pozostałe podpunkty?

geometrykz: tak

Eta: Ciekawa jestem jak wyznaczałeś cosβ ?

geometrykz: obliczyłem sinus kąta ostrego: stosunek wysokości do boku; wyszło, że sinus to 54 stopnie; pomnożyłem 54 stopnie razy dwa i wyszło 108, co odjąłem od 360 stopni i wynik podzieliłem przez dwa. ze wzorów redukcyjnych wyznaczyłem odpowiedni kąt, i wyszło mi ~0,587 − dobrze to zrobiłem?

geometrykz: −0,587 **

geometrykz: i jak?

Eta: Źle , bo podajesz przybliżenia miar kątów P=32 z poprzedniego podpunktu

	4		3
P=a2*sinα ⇒ sinα=		, to cosα=
	5		5

	3
cosβ= cos(180o−α)= −cosα= −		= −0,6
	5

Eta: c) można też skorzystać z iloczynu skalarnego wektorów zaczepionych w punkcie B lub z tw. kosinusów w trójkącie ABC

geometrykz: ok, dziękuję, też mi sinus wyszedł 4/5, tylko robiłem to właśnie z tych przybliżeń