Wykaż, że jeżeli a,b ≥0 to √a+√b≤√2(a+b) Smerf: Wykaż, że jeżeli a,b ≥0 to √a+√b≤√2(a+b)

Eve: podnieś obie strony do kwadratu

Smerf: aha myślałem że jest też jakiś inny sposób, dzięki

Eve: nie ma

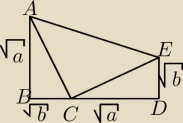
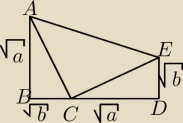diana7: Oczywiście, że jest inny dowód. Rozważmy trójkąty prostokątne ABC i CDE o przyprostokątnych odpowiednio AB=√a, BC=√b, CD=√a, DE=√b. Załóżmy ponadto, że punkty B, C, D leżą na jednej prostej. Łatwo pokazać, że kąt ACE jest prosty, zatem z tw. Pitagorasa mamy AC=CE=√a+b oraz AE=√2(a+b). Ponieważ BD jest równe odległości prostych DE i AB, więc AE ≥BD.