Pomocy prosze
:): Trójkąt wpisany w kwadrat − udowodnienie.
W kwadrat ABCD o boku 2 wpisano trójkąt równoramienny AEF tak, że wierzchołek E leży na boku
BC, a wierzchołek F− na boku CD oraz |AF|=|EF|. Niech x=|BE|.
Wykaż, że funkcja
| | 1 | |
P(x)=2− |
| x(x−2)2 opisuje pole trójkąta AEF dla x∊<0,2>. |
| | 8 | |
29 sty 23:56
:):
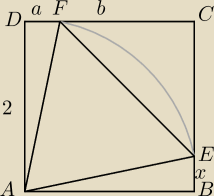
Ktoś pomoże, wytłumaczy co i jak ?

30 sty 00:02
Bogdan:
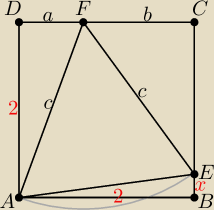

30 sty 00:20
:): 
, ale jak to obliczyć

30 sty 00:22
Bogdan:
b = 2 − a
Pitagoras.
ΔADE: 4 + a
2 = c
2
ΔECF: (2 − x)
2 + (2 − a)
2 = c
2
| | 1 | |
4 + a2 = (2 − x)2 + 4 − 4a + a2 ⇒ 4a = (2 − x)2 ⇒ a = |
| (2 − x)2 |
| | 4 | |
| | 1 | | 1 | | 1 | |
ΔAEF: Pole P = 22 − ( |
| *2*a + |
| (2 − a)*(2 − x) + |
| *2*x) = ... |
| | 2 | | 2 | | 2 | |
kontynuuj
30 sty 00:40
:): Dzięki

7 lut 22:18
geo ana: Można prosić o dokończenie? Nie wychodzi mi ten u gory wzor ...
23 lut 13:49
geo ana: =4−(a+1/2(4−2x−2a+ax)+x)=4−(a+2−x−a+1/2 ax+x)=4−a−2+x+a−1/2 ax −x=2−1/2 ax

?
23 lut 14:11
Eta:
| | 1 | | 1 | |
P(x)= 2− |
| ax i a= |
| (2−x)2 |
| | 2 | | 4 | |
podstawiając za a otrymasz
| | 1 | | 1 | |
P(x)= 2− |
| * |
| (2−x)2*x = ............ |
| | 2 | | 4 | |
23 lut 17:33
mar: Odnawiam zadanie, bo ja mam jeszcze dalszą część.
Muszę policzyć minimalne i maksymalne pole trójkąta AEF.
17 kwi 09:50
wredulus_pospolitus:
I w czym problem? Skoro już wykazałeś jak wygląda funkcja opisująca pole tegoż trójkąta

17 kwi 09:55
mar: Nie jestem pewien jak to zrobić... mam policzyć pochodną funkcji P i zobaczyć gdzie jest
mniejsza, a gdzie większa od i tam gdzie będą odpowiednie ekstrema, tam będzie największe i
najmniejsze pole o ile łapie się w dziedzinie?
17 kwi 09:57
wredulus_pospolitus:
1. pochodna
2. szukasz ekstrem funkcji f(x) czyli sprawdzasz f'(x) = 0 (i wybierasz tylko te które leżą
wewnątrz badanego przedziału)
3. wyznaczasz wartość funkcji f(x) w tychże punktach oraz f(0) oraz f(2)
Porównujesz wartości ... wybierasz najmniejszą i największą
17 kwi 10:01
mar: OK
| | 3 | |
P'(x)=− |
| x2 + x + 1/2 = 0 |
| | 8 | |
| | 4+2√7 | |
x1 = |
| = 3,09 nie należy do [0,2] |
| | 3 | |
| | 4−2√7 | |
x2 = |
| = −0,45 ne należy do [0,2] |
| | 3 | |
P(0)=2
P(2)=2
czyli niezależnie od x zawsze pole tego trójkąta zawsze będzie równe 2.
17 kwi 10:19
mar: Ale jak się zastanawiam jakby miał wyglądać taki wykres, gdzie w −0,45 mamy min, a w 3,09 mamy
max to chyba nie powinna wyjść taka sama wartość na krańcach przedziału [0,2]...
17 kwi 10:38
mar: źle pochodną policzyłem, powinno być:
| | 3 | |
P'(x)=− |
| x2 + x − 1/2 = 0 |
| | 8 | |
x
1 = 2 − maximum y
max = 2
x
2 = 2/3 − minimum y
min = 50/27
P(0)=2
P(2)=2
Czyli najmniejsze pole będzie dla x=2/3 i wynosi 50/27, a największe dla x=0 i x=2 i wynosi 2.
Teraz mi się wszystko zgadza.
17 kwi 10:59
 Ktoś pomoże, wytłumaczy co i jak ?
Ktoś pomoże, wytłumaczy co i jak ? 


 , ale jak to obliczyć
, ale jak to obliczyć

 ?
?
