|(x+6)/(x+3)|=(1/4)^(m+5) i m ∊ R Norbercik 125: Trzeba w zależności od parametru m powiedzieć kiedy podane równianie ma więcej rozwiązań ujemnych niż dodatnich z góry dziękuje za pomoc |(x+6)/(x+3)|=(1/4)⁽m+5) i m ∊ R po prawej stronie jest (1/4) do m+5

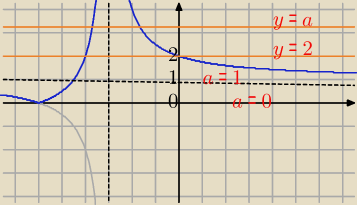
Tadeusz: nie zapomnij że ta stała to y=0,25^m+5

Bogdan:

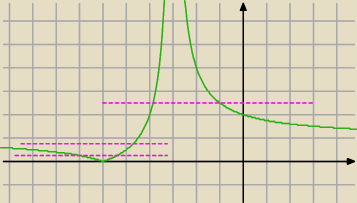
	x + 6
y = |		| funkcja homograficzna pod wartością bezwzględną
	x + 3

	1
y = a, gdzie a = (		)m+5 funkcja stała, wykresem jest linia prosta równoległa
	4

do osi odciętych Widzimy, że dla: a = 0 jest jedno rozwiązanie ujemne, a∊(0, 1) są dwa rozwiązania ujemne a = 1 jest jedno rozwiązanie ujemne a∊(1, 2) są dwa rozwiązania, jedno ujemne i jedno dodatnie itd.

Bogdan: Przepraszam Tadeuszu, pisząc swój post nie widziałem Twojego

Tadeusz: ... ależ nie ma za co − Pewnie łątwiej będzie mu to "przetrawić" −

pigor:

	x+6		1
..., dla jakich wartości parametru m równanie |		| = (		)m+5
	x+3		4

ma więcej pierwiastków ujemnych niż dodatnich ? −−−−−−−−−−−−−−−−−−−−−−−−−−− otóż, w granicy lim _{x → −∞} |^x+6_x+3|= lim _{x → −∞} |1+³_x+3|= 1, więc warunki zadania spełniają nierówności 0< (¹₄)^m+5< 1 ⇔ ⇔ m∊R i 4^−m−5< 4⁰ ⇔ −m−5< 0 ⇔ m > −5 ⇔ m∊(−5;+∞). ...

pigor: ... , mam źle; sknociłem sprawę ; przepraszam ...

pigor: ... . lub (¹₄)^m+5 >2 ⇔ ... . ..

Norbert: Okej, czy jest jakiś inny sposób niż rysowanie? Np zrobić to algebraiczne? Tak czy siak, dziękuję